I. ОСНОВЫ ПРОСТРАНСТВЕННОГО АНАЛИЗА
1. КОНЦЕПТУАЛИЗАЦИЯ ПРОСТРАНСТВЕННЫХ ОТНОШЕНИЙ
1.1. Геопространственный анализ
Американскому профессору статистики и консультанту по менеджменту Уильяму Эдвардсу Демингу (W. Edwards Deming) приписывают замечательное в своем роде выражение "В Бога мы веруем. Все остальные пусть предоставят данные", смысл которого заключается в том, что без настоящих данных и работы с ними невозможно постижение истины. Наблюдения и измерения, параметры и характеристики (т.е., данные) - лежат в основе любого современного исследования и давно уже стали неотъемлемой частью управления, что, возможно, особенно ярко проявилось в самые последние годы в связи с разными кризисами: экономическими, экологическими, наконец - в связи с пандемией. Без надежных и правильным образом обработанных данных нет "доказательной науки", следовательно, нет и адекватной реакции, корректного управления ситуацией.
Статистика, как раздел математики, посвященный работе с данными, как известно, появилась не вчера, однако с момента изобретения географических информационных систем (ГИС) возникла возможность привязывания данных к местоположению - возможность, обогатившая географию методами так называемого пространственного анализа. Огромные массивы непространственных данных, получив координатную привязку, стали "работать" на объяснение в географии, что привело к пересмотру многих традиционных представлений и появлению новых теорий.
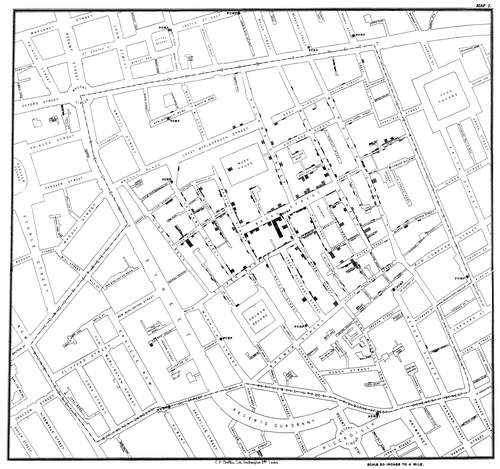
Рис. 1.1 Карта Джона Сноу (1854 г.), на которой отмечены случаи холеры и водозаборные колонки
Можно возразить, что интуитивный пространственный анализ существовал и ранее: достаточно вспомнить интригующую историю про открытие источника холеры в Лондонском Сохо Джоном Сноу, составившим карту (Рис. 1.1), на которой были отмечены места расположения водоразборных колонок и дома с заболевшими и умершими от холеры. Предполагается, что анализ увеличения плотности точек вблизи колонок привел врача к выводу об источнике возбудителя заболевания. Но согласимся - только относительно недавно мы получили возможность "привязывать" сотни тысяч и даже миллионы объектов и событий к географической "подоснове" и заниматься геопространственной статистикой.
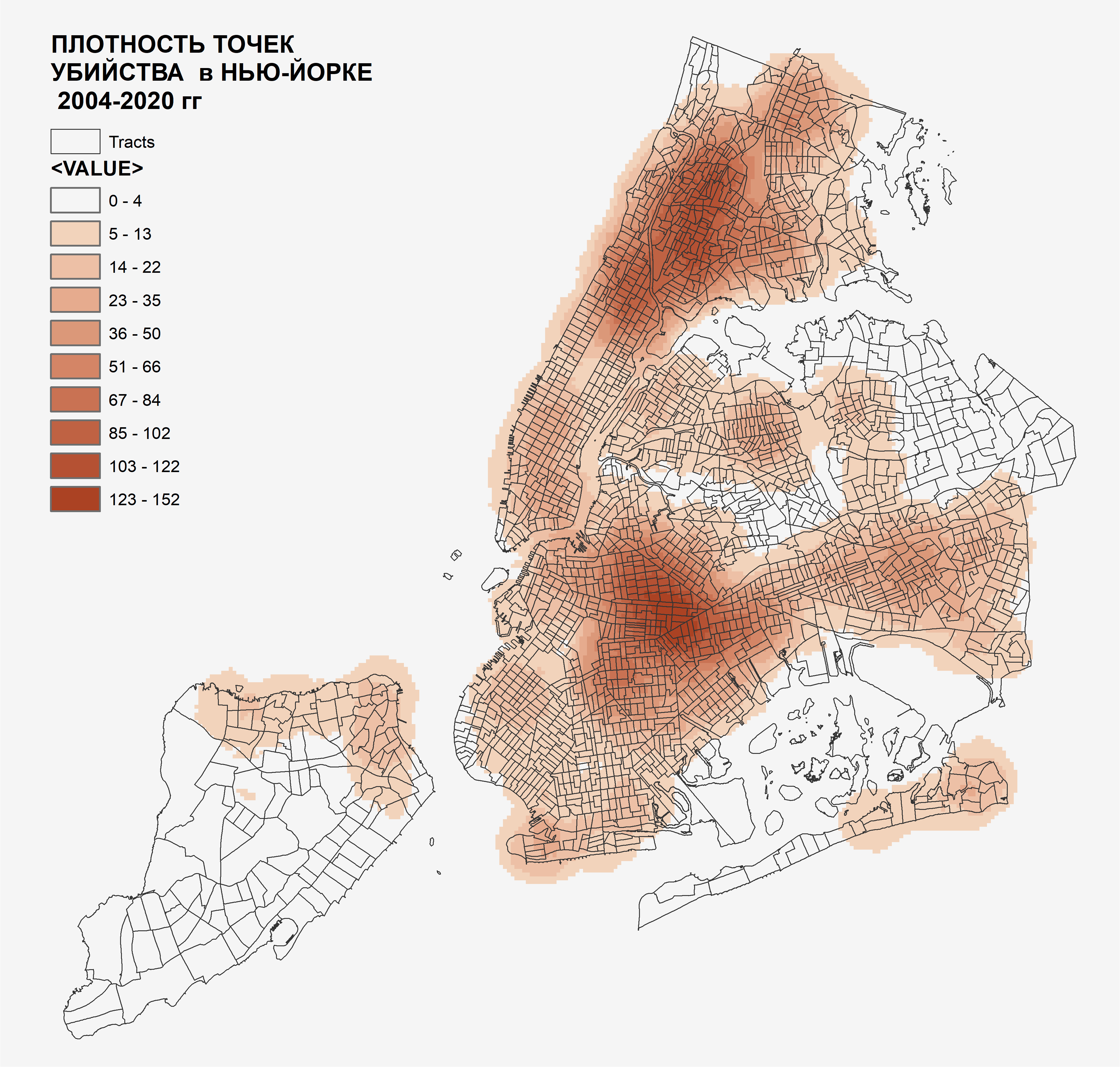
Геопространственный анализ позволяет отображать множество отдельных событий (например - преступления, заболевания), так и множество различных свойств в пределах разных операционно-территориальных единиц (ОТЕ); например - преступность или заболеваемость в границах отдельных районов или кварталов города (Рис. 1.2).

Рис. 1.2 Онкологические заболевания (2005-2009) по кварталам Нью-Йорка (фрагмент) как пример отображения явления по матрице операционно-территориальных единиц
Согласно Л. Анселину [Anselin, 1989, стр. 2] пространственный анализ - это количественное изучение пространственно распределенных явлений. По П. Лонгли с соавторами пространственный анализ - это "процесс, посредством которого мы превращаем необработанные данные в полезную информацию в погоне за научными открытиями или более эффективным принятием решений" [Longley et al., 2011, p. 17]. Одно из последних определений принадлежит Г. Грекоузису : "пространственный анализ - это совокупность методов и статистических данных, которые объединяют такие понятия, как местоположение, площадь, расстояние и взаимодействие, для анализа, исследования и объяснения в географическом контексте" [Grekousis, 2020, p. 2.].
Так или иначе на сегодняшний день пространственный анализ это уже целая научная сфера которая включает [O’Sullivan, Unwin, 2010, p.3]:
- манипулирование пространственными данными с помощью географических информационных систем (ГИС),
- анализ пространственных данных описательным и исследовательским способом,
- пространственную статистику, которая использует статистические процедуры для получения "объясняющих" выводов и причинно-следственных связей,
- построение моделей для выявления взаимосвязей и прогнозирования результатов в пространственном контексте.
Методы пространственного анализа вносят ценный вклад в понимание как природных, так и социальных систем. В геоэкологии методы пространственного анализа могут быть применены в исследованиях самого широкого спектра природных явлений и процессов - от изменения глобального и регионального климата, до исследований геохимических полей, определения направленности и скорости неблагоприятных процессов экзогенной геодинамики, изучение загрязнения воздушного бассейна городов, оценки изменения ландшафтных метрик, характеризующих структуру природной среды и т.д. В экономике методы пространственного анализа могут быть использованы для анализа, картографирования и моделирования взаимосвязей между людьми и различными аспектами экономической жизни; таким образом мы можем изучать различные причины бедности, социального неравенства и т.д.. В социальных исследованиях пространственный анализ может оказаться полезным в изучения того, как люди взаимодействуют в социальном, экономическом и политическом контекстах, что позволяет, например, выявить причины преступности и девиантного поведения.
В отечественной практике ГИС-моделирования термин Пространственный Анализ появился как прямой перевод англоязычного термина Spatial Analysis, в этой связи не всегда легко провести различие между пространственным анализом и географическим или геопространственным анализом, тем более, что все три термина использовались множеством авторов в самых различных контекстах. В общем случае термин географический (или геопространственный) анализ относится к поверхности Земли с ее характерным рельефом суши, растительным покровом и акваторией Мирового Океана. Пространственный Анализ, вероятно, несколько шире, поскольку он может относится к разным типам объектов (например - к другим планетам), и, что важнее - к разным категориям пространств. Так для анализа визуальных свойств фрагментов городской среды (общественных пространств или кварталов с домами) важно представлять ее как совокупность трехмерных объемов, с экранирующими взгляд плоскостями и диапазонами развертки так называемых "вист" (вееров оптических осей созерцания). Подобный анализ в большей степени "пространственный" чем "географический", не случайно для его реализации существуют специальное программное обеспечение Depthmaps.
Основным преимуществом пространственного анализа является способность выявлять закономерности, которые ранее не были определены или даже не наблюдались. Например, используя методы пространственного анализа, можно определить кластеризацию возникающих заболеваний, а затем разработать механизмы для предотвращения его распространения. Точно также можно выявить причины наступающей ксерофитизации растительного покрова в регионе, факторы пожароопасности или заболачивания лесов и т.д. В этом отношении пространственный анализ приводит к лучшему принятию решений в пространственном планировании [Grekousis, 2019]. Не случайно многие методов пространственного анализа, например - MSPA|Структурный анализ все чаще включаются в арсенал инструментов архитектурного проектирования, градостроительства и районной планировки.
В широком смысле существует четыре типа пространственного анализа:
1) Анализ точечных данных с целью выявления одного из трех типов распределений: кластерного, рассеянного, случайного
. Классический пример - распределение преступлений или заболеваний. Относительно обоих этих феноменов непустым является вопрос распределены ли они случайно или сгруппированы в кластеры или образуют некую другую, возможно - регулярную мозаику ("паттерн"). В случае обнаружения кластеров мы можем задаться следующим вопросом: какие факторы (экологические для заболеваемости и социальные - для преступности) могут служить причинами формирования кластеров? Анализ распределения точек также включает в себя различные меры центральности - так называемую центрографику - набор статистических переменных, используемых для определения центральных мест и выявления причин явления.2) Пространственный анализ для полигональных (ареальных) данных, используемый для индивидуального и типологического районирования, а также для конфигурирования различного рода зональных сущностей как естественных (природных зон, экорегионов) так и социальных (участков переписи, почтово-индексных кварталов, планировочных городских районов, функциональных территориальных зон. Пространственная статистика помогает выявлять пространственную неоднородность и пространственную зависимость, демонстрируя, например, как группируются кварталы с различным уровнем доходов или как кластеры экорегионов с различными биоклиматическими показателями объединяются в природно-ландшафтные зоны. Таким образом, регионализация выступает основным проявлением концептуализации пространства в этом виде анализа.
3) Анализ геостатистических (непрерывных) данных можно считать частью теории поля, поскольку этот раздел статистики позволяет анализировать и моделировать непрерывные покрытия и гриды. Сюда можно отнести преобразования, проводимые над цифровыми моделями рельефа с целью получения геоморфометрических переменных (например, уклона и экспозиции). С геостатистикой связывают также интерполяцию, применяемую для заполнения разрывов в данных, таким образом например, обработкой данных многих сотен наземных метеостанций получают растры климатических переменных (например, среднегодовых температур или индекса влажности).
4) Пространственное моделирование (в узком смысле) иногда считают отдельным видом пространственного анализа, относя к нему причинно-следственный (например - регрессионный анализ) и так называемую пространственную эконометрику
[Grekousis, 2020].Все виды пространственного анализа имеют дело с пространственными данными. В свою очередь, пространственные данные относятся к пространственным объектам, которые обладают геометрическими параметрами и пространственной привязкой, но которые также могут характеризоваться и другими непространственными атрибутами [Bivand et al., 2008, p. 7]. Например, мы можем описать сельскую местность по целому спектру данных, характеризующих землепользование, социальную инфраструктуру и экологическую ситуацию, включив в разрабатываемую модель данные о локализации и планировочной структуре населенных пунктов, структуре сельскохозяйственных угодий, конфигурации дорожной сети, размещению социальных объектов (дошкольных учреждений, школ и больниц), локализации пожарных депо, контейнерных площадок для ТБО, сохраняющихся природных ландшафтах, и так далее. Когда эти данные связаны с местоположением с помощью пространственных атрибутов (координат, адресной системы), мы получаем пространственные данные с которыми можно оперировать различным образом - в зависимости от изучаемой проблемы.
Представление объектов в рамках геоинформационного моделирования достигается комбинированием данных двух типов: векторных геометрических примитивов с "подшитыми" атрибутами и так называемых полей - непрерывных мозаик растровых данных. Геометрические примитивы включают точки, полилинии и полигоны, за которыми в разных масштабах могут закрепляться разные семантики. Так точка может отображать отдельное дерево в модели крупного масштаба, биогруппу - в модели среднего масштаба или островной массив леса в мелкомасштабной модели. Точно также полигон может соответствовать отдельному строению, кварталу или целому населенному пункту. Поля (fields) презентуют объекты и явления как поверхность с непрерывно меняющимися свойствами: таковы поверхности рельефа (ЦМР), климатические характеристики или растры так называемых ландшафтных метрик.
Атрибуты или переменные - это взаимозаменяемые термины, обозначающие любую характеристику, которой может обладать тот или иной объект (например площадь, высота, уровень содержания гумуса в почве и т.д.). Конкретное выражение переменной принято называть значением.
1.2. "Что", "Где" и "Почему" - три этапа геопространственного моделирования
В руководствах по использованию пакета ArcGIS, разработанных известной американской компанией ESRI, традиционно предлагается рассматривать процесс пространственного анализа как рабочую последовательность, включающую постановку вопросов "What|Что", "Where|Где" и "Why-How|Почему". Этой последовательности соответствуют три раздела пространственной статистики: Descriptive Statistics|Дескриптивная Статистика, Exploratory Spatial Data Analysis|Исследовательский Анализ Пространственных Данных и, собственно, Inferential Statistics and Spatial Statistics|Выводная Статистика и Пространственное Моделирование. "Рабочей" эту последовательность делает простое обстоятельство невозможности приступить к последующему разделу не пройдя предыдущего.
На вопрос "Что?" можно получить ответ с использованием методов дескриптивной (описательной) статистики (Таблица 1.1), которая позволяет охарактеризовать данные, выявить характер распределения данных (нормальное, экспоненциальное, "паретианское"), обнаружить выбивающиеся значения (выбросы). Дескриптивная статистика использует карты (векторные и растровые слои ГИС) (Рис. 1.3), таблицы, графики, простые статистические процедуры для обобщения конкретной выборки (допустим - мест совершения преступлений в границах городского района), по этой причине ее результаты не являются репрезентативными для характеристики более обширного множества (преступлений в границах всего мегаполиса).

Рис. 1.3 Места ("точки") совершения преступлений в Нью-Йорке в кварталах Куинса за 2021 г. как пример отображения явления в рамках дескриптивной статистики
Таблица 1.1 ГИС-инструментарий дескриптивного анализа, задачи и использование