I. ОСНОВЫ ПРОСТРАНСТВЕННОГО АНАЛИЗА

3. ИССЛЕДОВАТЕЛЬСКИЙ АНАЛИЗ ДАННЫХ

3.1. Набор переменных для изучения феномена преступности в Нью-Йорке

Исследовательский анализ данных рассматривается в данном разделе на примере двух феноменов (или явлений) - преступности и заболеваемости в Нью-Йорке. Показатели, отражающие эти феномены выступают в выстраиваемой здесь модели как зависимые переменные; их называют также переменная-отклик, объясненная переменная и обычно обозначают как Y-переменные. Остальные переменные будут привлекаться как независимые переменные (факторы, или предикторы или объясняющие X-переменные). Понятно, что зависимые переменные в одном исследовании могут выступать как независимые (объясняющие) в другом [Бослаф, 2015].

Для демонстрации возможностей исследовательского анализа (ESDA) мы будем использовать файл кварталов tracts Нью-Йорка, полученный из стандартного файла NYCTRACTs.shp [New York City Census Tracts (2020 US Census)], а также файла NYC_Tract_ACS2008_12 с добавленными из различных источников и специально рассчитанными переменными (Таблица 3.1).

Таблица 3.1 Переменные, используемые для геопространственного анализа в модели Нью-Йорка

Этно-демографические факторы
№	Поле	Description	Описание
1	poptot	Total Population	Общая численность населения
2	popdty	Population Density (per sq. km	Плотность населения (чел. на км₂)
3	medianage	Total Population Median Age	Средний возраст жителей
4	european	Total Population White	Общая численность белого населения
6	african	Total Population African American	Общая численность афроамериканского населения
7	otherethni	TTotal Population Other Race	Общая численность этнического населения (не белых американцев)
Образовательный ценз
8	onlyhighsc	Population 25 Years and over with educational attainment of only high school level	Население в возрасте 25 лет и старше с образованием на уровне средней школы
9	onlybachel	Population 25 Years and over with educational attainment of a bachelor’s level degree	Население в возрасте 25 лет и старше с образованием на уровне бакалавра и ниже
10	onlydoctor	Population 25 Years and over with educational attainment of doctorate level degree	Население в возрасте 25 лет и старше с образованием на уровне докторской степени
Характеристика домохозяйств
11	households	Total Households	Общее число домохозяйств
12	okay	Doing okay as regards Ratio Of Income In 2012 To Poverty Level (2.00 and over)	Домохозяйства с уровнем доходов выше Уровня Бедности (2,0 $ в день и выше)
13	poororstru	Poor or struggling as regards Ratio Of Income In 2012 To Poverty Level (Under 2.00)	Бедные или испытывающие трудности домохозяйства на Уровне Бедности (Менее 2,0 $ в день)
14	poor	Doing poorly as regard Ratio Of Income In 2012 To Poverty Level (Under 1.00)	Домохозяйства ниже уровня бедности (менее 1,0 $ в день)
15	Income	Median household income (In 2012 Inflation Adjusted Dollars)	Средний доход домохозяйства (Приведенный к уровню инфляции доллара)
16	Gini_Ind	MGini Index Of Income Inequality	Индекс неравенства доходов Джини
Уровень безработицы
17	UEMPRATE	Unemployment rate	Доля безработных лиц трудоспособного возраста к общей численности трудоспособного населения
18	europeanun	European American unemployed population	Евро-американское безработное население
19	africanune	African American unemployed population	Безработное население афроамериканцев
Плотность и высотность застройки
20	SUM_shape*	Plan footprint	Суммарная площадь оснований зданий и строений
21	SUM_height*	Accumulated height of all buildings in the tract	Накопленная высота всех зданий квартала
22	SUM_height*square	Plan footprint	Накопленный объем всех зданий квартала
Некоторые параметры комфортности среды
23	BicyclL*	Total length of bike lanes	Суммарная длина велосипедных дорожек
24	WaterS*	Total area of water areas	Общая площадь акваторий
25	Park*	Total area of parks	Общая площадь парков
Уровень преступности
26	Mudr_15y*	The number of murders in 15 years (2015-2020)	Число убийств за 15 лет (2015-2020)
27	Crime_15y*	Total number of crimes in 15 years (2015-2020)	Общее число преступлений за 15 лет (2015-2020)
Уровень онкологической заболеваемости
28	CancTot*	Total number of observed cancer cases	Общее число зарегистрированных онкологических заболеваний
29	CancLung*	Total number of observed lung cancer cases	Общее число зарегистрированных заболеваний рака легких и бронхов

* "звездочкой" помечены дополнительно рассчитанные параметры

3.2. Базовые статистики одномерного исследовательского анализа

Чтобы получить представление о переменных необходимо прежде всего выявить характер их распределения в пространстве города с помощью Картограммы хороплет и Гистограммы частот.

Число самых тяжких преступлений против личности - убийств - для Нью-Йорка обнаруживает неравномерное распределение, поскольку мы можем наблюдать некое подобие кластеров "криминальных" кварталов (Рис. 3.1) на территории Бронкса и Бруклина.

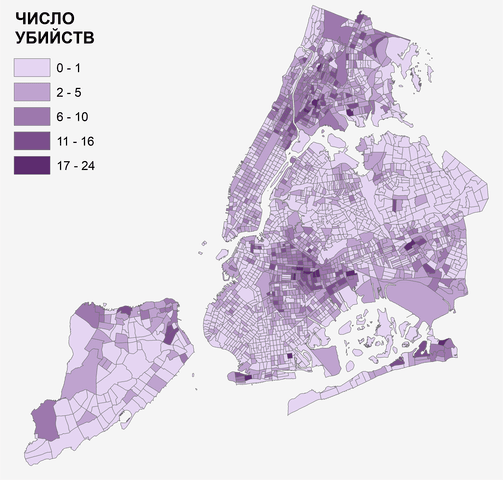
Рис. 3.1 Общее число убийств за 15 (2005-2020) лет по кварталам Нью-Йорка

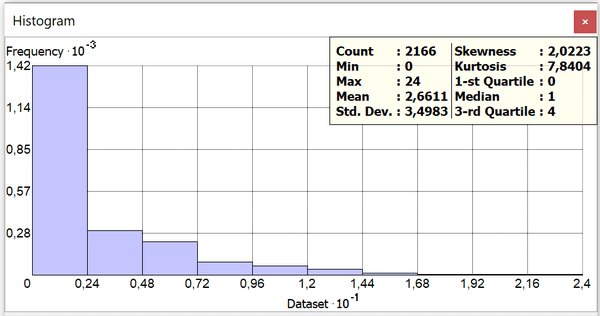
Гистограмма - графическое представление распределения частот для количественного признака, образуемое соприкасающимися прямоугольниками, основаниями которых служат интервалы классов, а площади пропорциональны частотам этих классов (ГОСТ Р 50779.10-2000) позволяет верифицировать это предположение.

Рис. 3.2 Гистограмма распределения убийств по кварталам Нью-Йорка

Известно, что для нормальных распределений, вне зависимости от их среднего значения и стандартного отклонения характерны такие свойства как симметричность, непрерывность значений, равенство или близкие значения среднего медианы и моды, а также присутствие единственного наиболее частого общего значения - унимодальность [Бослаф, 2015]. Таким образом, анализируя вычисленные в ArcMAP10.x вместе с построением гистограммы значения основных статистик можно сделать важные выводы о характере распределения переменной.

Skewness|Скошенность (асимметрия) определяет симметричность распределения, а ее показатель определяет где лежит большинство конкретных значений переменной относительно среднего арифметического - слева (т.е., в области меньших значений), или справа (в области больших значений); при этом асимметрия нормального распределения близка к нулю. Отрицательные значения асимметрии сопровождаются Kurtosis|Эксцессом вправо, соответственно самая высокая повторяемость значений ("бин" или столбик гистограммы) находится справа от среднего, а медиана больше, чем среднее. Наоборот, положительные значение асимметрии означают эксцесс влево (в сторону меньших значений), где находится самая высокая повторяемость значений, при этом правый хвост длиннее левого и медиана меньше, чем среднее арифметическое.

Кроме того, Kurtosis|Эксцесс характеризует плотность распределения и вероятность выбросов. Распределения с положительными значениями эксцесса имеют "тяжелые хвосты" и называются "островершинными". Отрицательные значения эксцесса соответствуют плосковершинным распределениям и имеют "тонкие хвосты". Эксцесс нормального распределения равен трём [Создание и использование гистограмм].

Очевидно, что распределение убийств в Нью-Йорке далеко от нормального: бины-столбики максимальных частот прижаты к началу гистограммы (т.е., к низким значениям переменной), поэтому асимметрия положительна. Медиана почти втрое меньше среднего значения, также расположенного в левой части, стандартное отклонение более чем в три раза превосходит среднее, бины-столбики с максимальными значениями резко сдвинуты вправо - в область больших значений.

Поскольку в данной модели нас интересуют два явления - преступность и заболеваемость - имеет смысл выявить насколько конкретные проявления этих феноменов отличаются от общих, иными словами, отличается ли пространственное распределение убийств от преступности в целом, и есть ли какая-то специфика рака легких, которая отличала бы распространение этого диагноза от онкологических заболеваний в целом. Простой способ выявления отличий - сравнение гистограмм для "общего" и "частного"" признака.

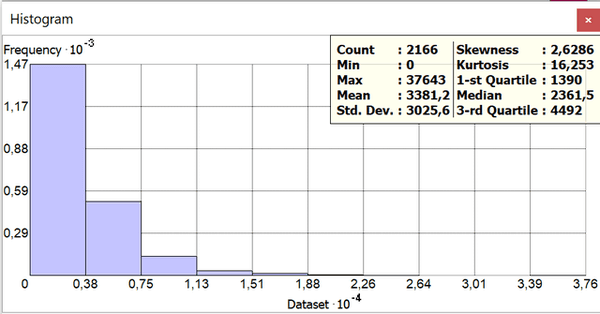
Рис. 3.3 Гистограмма распределения всех видов преступлений по кварталам Нью-Йорка

Несмотря на различия в абсолютных значениях между Общей преступностью и Числом убийств характер распределения обеих переменных аналогичен: перед нами логнормальный график с максимальным значением частот, прижатым к левой стороне гистограммы, средним значением значительно большим медианы, близкими показателями асимметрии распределения (2,0 - убийства, 2,6 - Общая преступность) и высокими значениями выбросов. Следовательно самые тяжкие преступления против личности вполне отображают общую картину преступности.

Альтернативный способ проверить наличие выбросов переменной, а также определить, соответствует ли переменная нормальному распределению - построение специального графика QQplot|КК-График(Квантиль Квантиль график): Explore Data >> Normal QQPlot >> Attribute = Mudr_15. КК-График для данной переменной показывает, что значения переменной Число убийств по кварталам отклоняются от прямой линии нормального распределения.

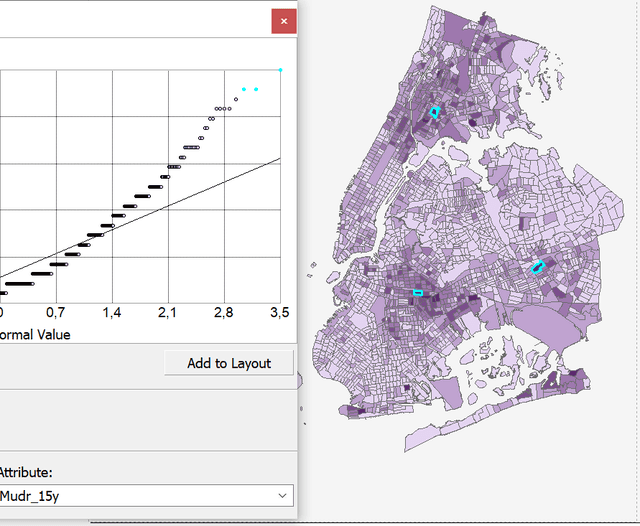
Рис. 3.4 Выделение крайних точек на QQ-графике с отображением на картограмме (хороплете)

Все графики и диаграммы Исследовательского Анализа связаны с объектами (полигонами - как в данном случае) шейп-файла и таблицей атрибутов слоя, что является одним из преимуществ использования инструментов ESDA в пространственном анализе. При выделении столбца на гистограмме, либо точек на QQ-графике и/или Диаграмме Размаха становятся выбранными соответствующие полигоны на карте и строки таблицы атрибутов. Поэтому, проведя стрелкой Select Features по точкам в крайнем правом углу графика, мы определяем кварталы, которые значительно отклоняются от линии ожидаемых (при нормальном распределении) значений (Рис. 3.4). Эти кварталы находится в центре ареалов концентрированного проживания афроамериканского населения, обстоятельство, которое может служить одним из предположений для выстраивания гипотезы пространственного анализа.

Следующий способ проверки распределения переменной - построение Box Plot|Ящичковой Диаграммы или как ее еще называют Диаграммы Размаха, еще одно наименование - "Ящик с Усами", происходящее от прямого перевода английского "box-and-whiskers diagram". Ящичковая диаграмма позволяет компактно отобразить одномерное распределение вероятностей.

Для построения Диаграммы Размаха выберем в главном меню:

Main Menu >> View > Graphs >> Create Graph
Graph type = Box Plot
Layer/Table = NYCTRACTs
Value field = Murd_15
>> Next >>
Title = Murders

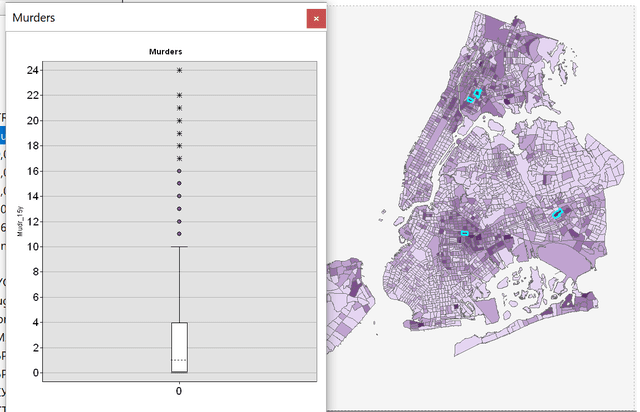
Рис. 3.5 Выделение выбросов значений числа убийств на Ящичковой Диаграмме (Box-Plot) с отображением на картограмме (хороплете)

На Диаграмме Размаха показаны шесть незначительных выбросов (одиннадцать и более убийств обозначены точкой) и семь экстремальных выбросов (более 16 убийств - обозначены звездочкой), относящихся к кварталам с высоким числом убийств (Рис. 3.5). Выбросы значений с низким уровнем убийств не отслеживаются, поскольку для многих кварталов это значение равно нулю. Ящичковые диаграммы на стадии Исследовательского Анализа служат прежде всего для проверки данных, т.е., для ответа на вопрос не являются ли выбросы просто ошибками соответствующего учета. Далее (в случае корректности данных) мы получаем возможность выстраивания предположений относительно: а) выявленной неравномерности распределения, и b) их возможной обусловленности теми или иными факторами. Отметим, что любые предположения на данном этапе могут оказаться спекулятивными - высокие значения фактора, например, могут оказаться связанными с высокой плотностью населения.

Наконец, еще один способ анализа распределения переменной - расчет так называемого Z-Score|Z-Значения (Z-Балла). Поскольку существует множество нормальных распределений, характеризующихся исходными данными различной размерности (и физической сущности), их характеризуют в терминах стандартного отклонения, избавляющих нас от перечисленной конкретики. Напомним, что Стандартное Отклонение - это квадратный корень из дисперсии или квадратный корень из среднего для квадратных отклонений от среднего арифметического. Для расчета Z-Значения необходимо предварительно добавить новое поле в таблицу щейп-файла (в нашем случае - файла NYCTRACTs):

Table of Content >> RC City >> Open Attribute Table Click at Table Options button >> Add Field
Name = MurdZScore
Type = Float Precision|Плавающая запятая = 5 (общее число цифр)
Scale = 3 (число цифр после запятой)
Z-Оценка рассчитывается с помощью Калькулятора Поля как разница между значением переменной минус частное от деления Среднего Арифметического на Стандартное Отклонение: относительно выбранной переменной
Z-Score = Murd_15 - 2,7 / 3,5

Полученные значения нового поля Z_Murd могут быть отображены на карте хороплета. Чем выше или ниже Z-оценка, тем больше разница между значением переменной (в данном случае - числом убийств) по кварталам и средним значением для всего исследуемого ареала. Значения выше 15 могут претендовать на выбросы (outliers). Очевидно, что различные определения выбросов приводят к несколько иным результатам. Сколько и какие выбросы в конечном итоге будут сохранены, зависит от задач анализа.

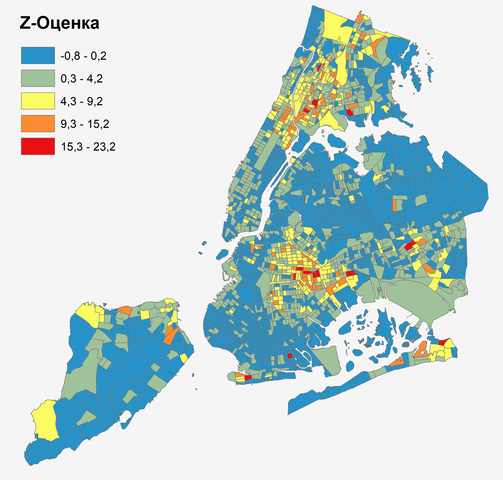
Рис. 3.6 Хороплет Z-Score отражает экстремально высокие значения переменной более наглядно, чем исходные данные

3.3. Характеристики переменных

Различные бытующие в общественном сознании концепции связывают уровень преступности с самыми разными факторами, среди которых - расово-этнические (компактное проживание представителей той или иной расы или этнического большинства), экономические (уровень благосостояния), личностные (например, уровня образования населения) и факторы комфортности городской среды (плотность и морфотипы застройки, присутствие зеленых насаждений и т.д.). Построим хороплеты и графики для имеющихся в нашем распоряжении факторов разных групп. Для начала оценим долю афроамериканского населения в общей численности населения по кварталам Нью-Йорка.

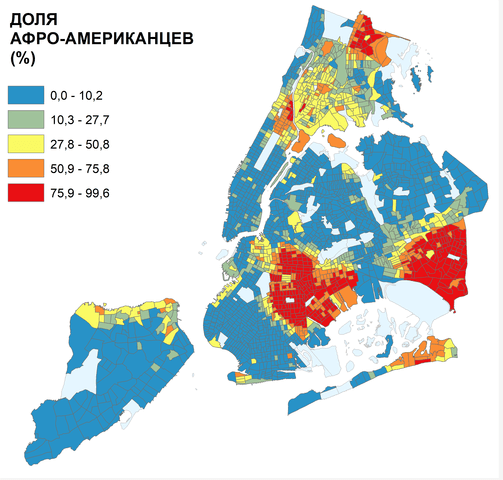
Рис. 3.7 Доля афроамериканского населения (%) по кварталам Нью-Йорка

Очевидно, что афроамериканцы живут в четырех отчетливо выделившихся ареалах: в центре Бруклина, на востоке Куинса, на северо-востоке и юго-западе Бронкса и узкой полосой на севере Статен-Айленда. Для построения гистограммы вызовем панель Geostatistical Analyst ArcMAP10.x. На появившейся панели выбираем Explore Data >> Histogram Select Layer = NYCTRACTs; Attribute = african.

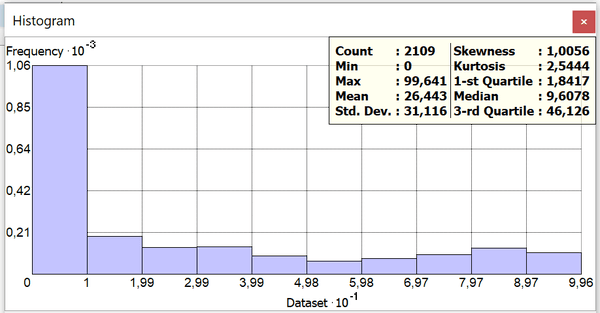
Рис. 3.8 Гистограмма доли афроамериканского населения в общей численности населения по кварталам Нью-Йорка

Гистограмма отображает базовую описательную статистику:

Результаты показывают, что распределение численности афроамериканцев по кварталам Нью-Йорка сильно искажено и значительно отклоняется от нормального. Гистограмма скошена влево, медианное значение значительно меньше среднего, частоты резко снижаются к противоположному от пика концу, значения первого и третьего квартилей сильно разнесены, эксцесс хорошо выражен. Осложняют общую картину и признаки "плато" между столбиками частот средних и максимальных значений.

Есть ли в представленном наборе переменных, характеризующих население и условия жизни в кварталах Нью-Йорка, нормально распределенные? Обратимся к такому показателю как Плотность застройки, (доля суммы оснований всех зданий и сооружений к площади всего квартала в процентах) в практике градостроительного планирования этот признак часто называют Запечатанностью.

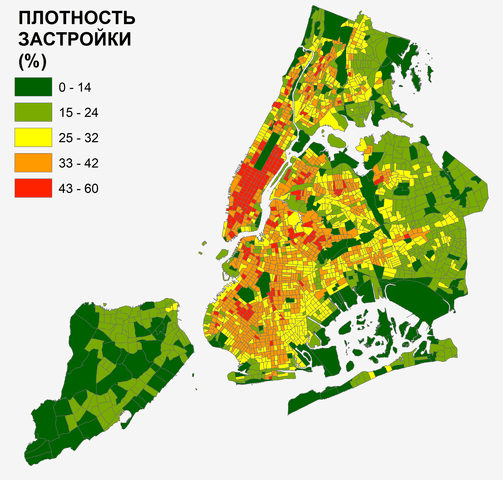
Рис. 3.9 Хороплет плотности застройки кварталов Нью-Йорка

Карта отображает высокую пространственную неоднородность и изменчивость признака: участки высокой плотности застройки приурочены, в основном, к острову Манхеттен, а также к отдельным ареалам Бронкса, в тоже время хорошо видны соседства с рыхлой или практически отсутствующей застройкой, прежде всего в пределах боро Статен-Айленд, богатом на парки и элементы зеленой инфраструктуры. Для выявления основных статистик построим гистограмму в ArcMAP 10.x.

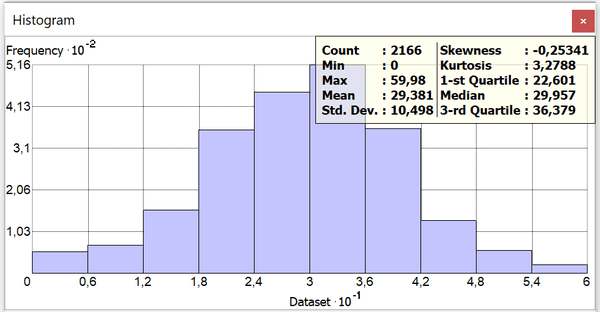
Рис. 3.10 Гистограмма распределения плотности застройки кварталов Нью-Йорка

Базовые статистики демонстрируют почти идеальное" нормальное распределение переменной: медианное значений практически совпадает со средним арифметическим, и совместно они образую вершину купола ("колокола") кривой распределения, обе стороны которой симметрично снижаются в сторону более высоких и более низких значений, поэтому и асимметрия крайне мала -0,25 (знак минус означает незначительный перекос в сторону больших значений).

Рассчитаем значения выбросов:

a) в большую сторону:
Mean + 2.5 * Standard Deviation
т.е., в данном случае
29,4 + 2.5 * 10,5 = 55,9
b) в меньшую сторону
Mean - 2.5 * Standard Deviation
29,4 - 2.5 * 10,5 = 3,15

Таким образом, в данных по параметру запечатанности кварталов Нью-Йорка выбросами могут считаться кварталы с плотностью застройки более 55,9% и менее 3,15%. Проверим эти выкладки на КК-Графике.

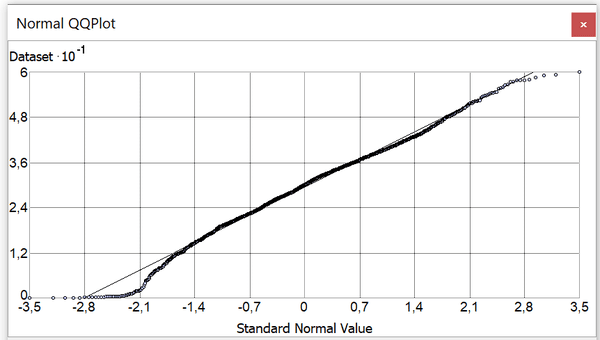
Рис. 3.11 КК-График для параметра плотности застройки кварталов

Кривая, образованная точками кварталов на КК-Графике переменной плотности застройки, почти идеально совпадает с тонкой линией нормального распределения. "Выбивающиеся" точки в верхней и нижней части кривой маркируют потенциальные выбросы, и мы можем выделить их вручную обведя соответствующие точки, либо использовать выбор по атрибуту с условием:
%Build > 55,9 or %Build < 3,15.
Выбранные таким образом полигоны хороплета совпадают с островными и парковыми кварталами Нью-Йорка, что объясняет причину их низкой застроенности.

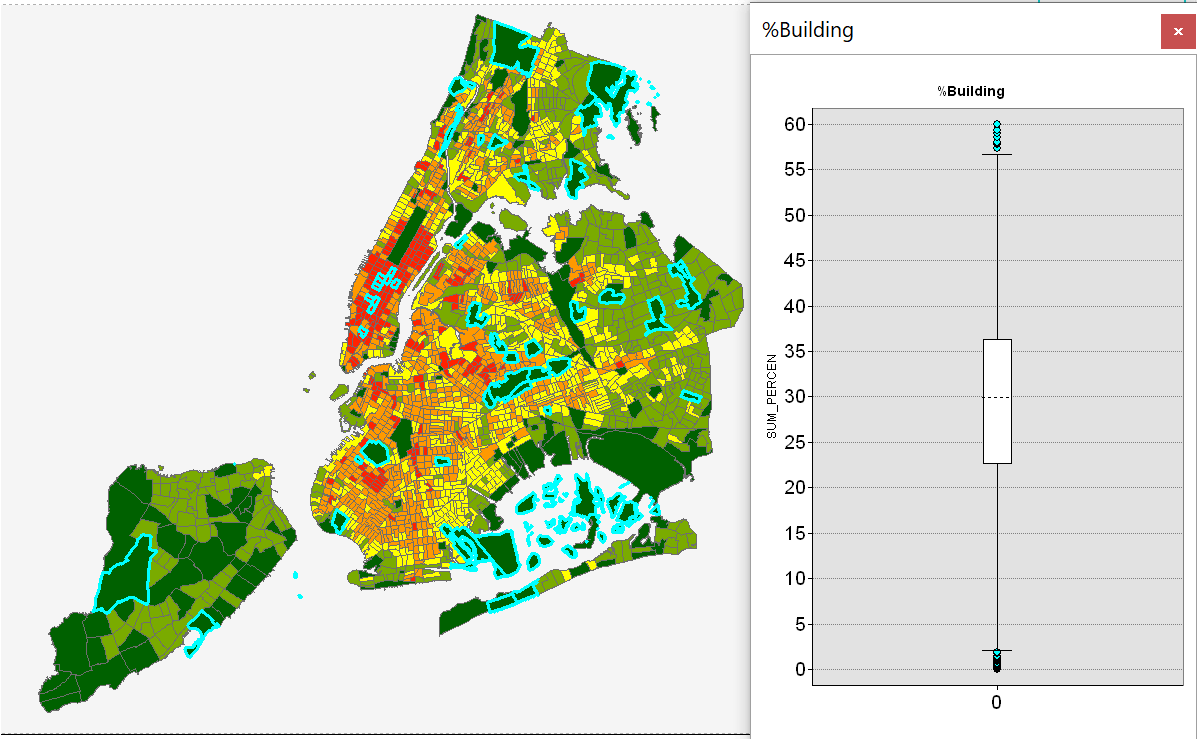
Рис. 3.12 Картограмма и Ящичковая Диаграмма для параметра плотности застройки с выбранными кварталами-"выбросами"

Последняя проверка - построение Ящичковой Диаграммы, которая демонстрирует почти точное попадание среднего значения на центр "ящика" и два выброса: верхние значения более 55,9 и нижние - менее 3,15, что совпадает с нашими расчетами. Таким образом, констатируем еще раз: переменная Запечатанность кварталов демонстрирует почти классическое нормальное распределение.

Среди прочих переменных, привлеченных для моделирования преступности и заболеваемости в Нью-Йорке, мы обнаружим различные типы распределений, часть из которых близка к логнормальному распределению, распределению Пуассона или биномиальному распределению.

Казалось бы, если дома — это прежде всего жилища для людей, то и переменная Плотность населения тоже должна быть распределена нормально. Для проверки построим гистограмму распределения для параметра Плотность населения по кварталам Нью-Йорка (Рис. 3.13).

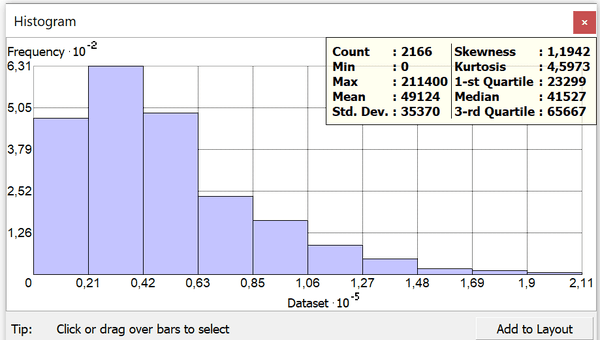
Рис. 3.13 Гистограмма плотности населения по кварталам Нью-Йорка

По характеру гистограммы плотности и основным статистикам (медиана - 41527 расположилась недалеко от среднего - 49124) мы можем видеть ассиметричное распределение, сдвинутое в сторону меньших значений (положительная "скошенность").

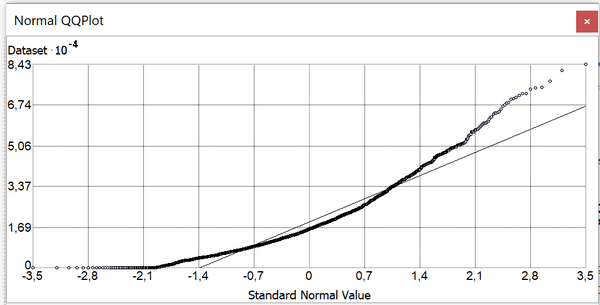
Рис. 3.14 КК-график для Плотности Населения по кварталам Нью-Йорка

Возможно, этот эффект объясняется весьма сильно различающейся этажностью морфотипов застройки: кварталы повышенной этажности аккумулируют заметно большее население. Для проверки данного предположения рассчитаем в новом поле Объемную Нагрузку|FootPrint как произведение площади застройки квартала на суммарную высоту всех зданий и сооружений.

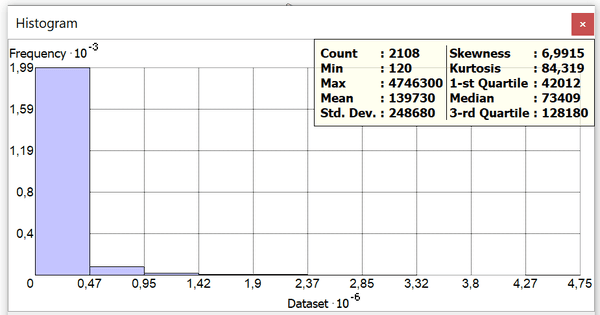
Рис. 3.15 Гистограмма Объемной Нагрузки FootPrint застройки по кварталам Нью-Йорка

Гистограмма демонстрирует все признаки ненормального "Head and Tail" (паретианского) распределения: значительно превышение среднего над медианой, высокая "перекошенность" графика в сторону меньших значений и далеко разнесенные значения первого и третьего квартилей. Таким образом, мы не можем ожидать "нормальности" и от переменной Плотность населения даже если предположить, что абсолютное большинство "скайскрепперов" — это офисные здания.

Сложное распределение демонстрируют и многие другие переменные нашей модели. Это касается как пространственного рисунка (паттернов случайности и неоднородности), так и частотного распределения.

Для сравнения посмотрим на распределение экономических переменных - например, Число домохозяйств ниже уровня бедности.

Рис. 3.16 Картограмма числа домохозяйств с доходами ниже уровня бедности (менее 1$ в день)

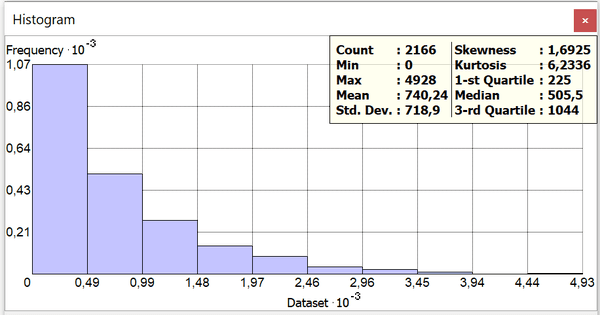
Рис. 3.17 Гистограмма распределения и домохозяйств с доходами ниже уровня бедности (менее 1$ в день)

Данный параметр демонстрирует почти классическое Head and Tail распределение со средним значением заметно большим медианы, "задранным" максимумом и длинным "сползанием" к "тяжелому хвосту" низких значений. Интересен и пространственный рисунок - несмотря на множество ареалов концентрации высоких значений, в общей мозаике можно уловить "кластерность".

Переменная Годового дохода домохозяйств выглядит совершенно иначе: распределение искажено небольшим перекосом в сторону низких значений, но при этом медиана 52118 $ близка к среднему 55654 $; вылеты, вероятно, определяются супервысокими максимальными значениями. На КК-Графике хорошо заметно, что отрыв от линейной функции в верхнем диапазоне начинается со значений 150 000 $, значения выше 170 000 $ - явные выбросы, в нижнем диапазоне отрыв от линейной функции около 30 000 $, выбросы - около 18 000 $.

Рис. 3.18 Хороплет Дохода Домохозяйств

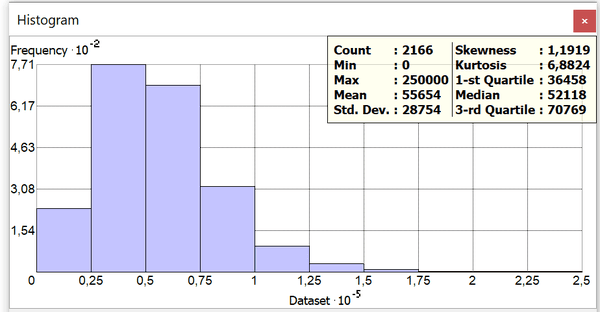
Рис. 3.19 Гистограмма распределения Дохода Домохозяйств

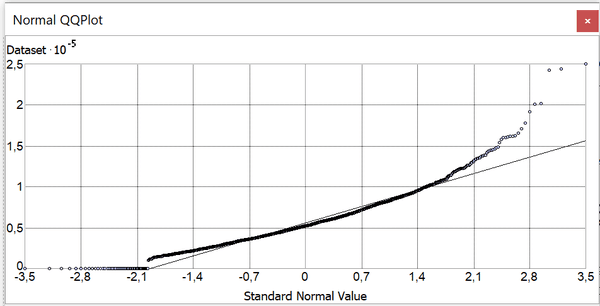
Рис. 3.20 КК-График распределения Дохода Домохозяйств

Таким образом, исследовательский анализ пространственных данных и связанные с ним инструменты обеспечивают всестороннее визуальное представление статистики путем связывания хороплетов (картограмм) с графиками, точечными диаграммами и гистограммами. В этой связке первый этап - составление картограммы, непростое искусство, предполагающее не просто визуализацию, но первичную классификацию данных, при этом выбор способа классификации должен быть оправдан свойствами и характером анализируемых данных. Вычисление базовых элементарных статистик - среднего значения, максимального и минимального значений, стандартного отклонения - обеспечивает начальное описание и презентацию распределения переменной.

Гистограмма распределения частот, а также Диаграмма размаха (Ящичковая диаграмма) и Kвантиль-Квантиль График в совокупности являются полезными инструментами визуализации типа распределения, а также обнаружения "вылетающих" значений переменной. В свою очередь обнаружение выбросов необходимо, поскольку дальнейший анализ может быть искажен, если выбросы не будут удалены или обработаны соответствующим образом.

Отдельный и непростой вопрос, возникающий в контексте анализа распределения - что делать если распределение не является нормальным? Здесь есть три решения:

Использовать непараметрическую статистику
Преобразовать ненормальное распределение в нормальное - выбор метода будет зависеть от знака и величины значения асимметрии (skewness);
Проверить размер выборки. Согласно центральной предельной теореме, которая гласит, что при определенных условиях по мере увеличения размера случайной выборки ее распределение приближается к нормальному распределению, мы можем использовать параметрическую статистику если выборка больше 30-40 объектов. Такое нарушение предположения о нормальности не вызывает серьезных проблем [Pallant, 2016]

Таблица 3.2 Трансформация данных, используемая для уменьшения асимметрии и нормализации данных

Характер асимметрии (Skewness)	Способ трансформации данных	Формула	Сюжеты применения
Высокая положительная	Обращение	Y_n = 1/Y	Обращение применяется, когда все значения положительны
Высокая положительная	Негативное Обращение	Y_n = - 1/Y	Обращение применяется, когда все значения положительны
Высокая положительная	Негативное Обращение	Y_n = - 1/Y, добавление 1 к отрицательным значениям в диапазоне от 0 до -1	Обращение используется для трансформации отрицательных значений
Высокая положительная	Взаимное Обращение	Для удельных показателей перестановка числителя и знаменателя, например, использование вместо параметра плотности (чел/га) обратного отношения (га/чел)	Взаимное обращение меняет порядок положительных значений: наибольшее становится наименьшим
Средняя или низкая положительная асимметрия	Извлечение квадратного корня из значений, либо логарифмическая трансформация	Y_n = Y^0,5 Y_n = LogY	Для данных с большим числом нулевых или ничтожных значений
Средняя или низкая отрицательная асимметрия	Возведение в квадрат	Y_n = Y² Y_n = LogY	Для данных с выраженным логарифмическим трендом
Высокая отрицательная асимметрия	Возведение в куб	Y_n = Y³ Y_n = LogY	Для данных с выраженным логарифмическим трендом

Нормализуем зависимые переменные - Общую преступность и Число онкологических заболеваний

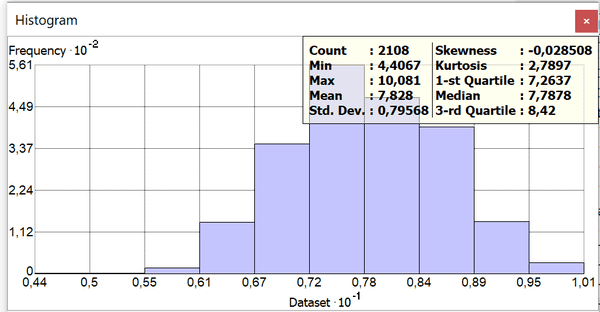
Рис. 3.21 Гистограмма распределения нормализованной переменной Общая преступность

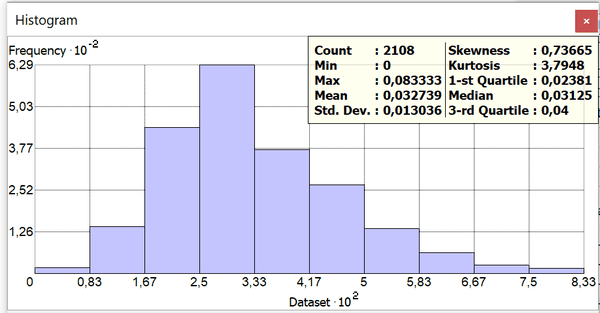
Рис. 3.22 Гистограмма распределения нормализованной переменной Число онкологических заболеваний

Сравним распределение с исходными переменными (Рис. 3.2) и (Рис. 3.3). Как можно видеть распределение значительно приблизилось к нормальному: при сохранившейся положительной (в сторону меньших значений) перекошенности медиана оказывается немногим меньшей среднего (5,2 против 5,3), очень заметно уменьшилось стандартное отклонение, сближены значения 1-го и 3-го квартилей.

3.4. Двумерный исследовательский анализ

Двумерный|Bivariate исследовательский анализ предоставляет нам начальную информацию об относительных взаимосвязях между любыми двумя переменными. Важно понимать, что на этом этапе моделирования мы не получаем доказанных причинно-следственных связей, а можем лишь делать предположения об их наличии или отсутствии. Остроумным предостережением в этом смысле является распространенный в зарубежной литературе статистический анекдот о связи между увеличением объема продаж мороженого и ростом числа жертв нападений акул на Атлантическом побережье США: как легко догадаться и то, и другое явление подчиняются началу и пику пляжного сезона, но при этом, разумеется, между поведением акул и успешностью реализации мороженого не существует никакой связи.

Тем не менее двумерный анализ позволяет сравнивать между собой распределение и пространственную неоднородность любой пары переменных. В нашем случае мы можем сравнивать две зависимые переменные (преступность и заболеваемость) с любыми из переменных привлеченных для моделирования. Один из способов такого сравнения - построение Диаграмма рассеяния|Scatter Plot.

В ArcMAP10.x выход на инструмент через Главное Меню: Main Menu >> View >> Graphs >> Create Graph >> Graph type = Scatter plot. На входе - "подопытный файл" кварталов Нью-Йорка NYCTRACTs. В Диаграмме рассеяния две оси для предположительной зависимой переменной Yз и независимой переменной (фактором) X, это обстоятельство позволяет сравнивать интересующие нас феномены (преступность и заболеваемость) с любыми факторами, которые, предположительно, могут оказывать на них влияние. Сравнение помогает отбирать факторы в качестве "кандидатов" на более серьезное моделирование и постепенно выстраивать гипотезу (или гипотезы) модели. Также, как и на любом другом графике, в ArcMAP10.x мы можем выделить необходимые кварталы просто обведя экстремально высокие точки на Диаграмме рассеяния. Это позволяет увидеть географическую локализацию объектов, и понять насколько высокие (или наоборот - низкие) значения по оси зависимой переменной Y соответствуют значениям независимой переменной X.

Построим Диаграмма рассеяния для Общей преступности (за 15 лет) и некоторых факторов, которые, как нам представляются, могут влиять на этот показатель. Для начала возьмем Индекс неравенства доходов Джини (значения которого находятся в диапазоне от 0 до 1: если доходы распределены равномерно, то показатель будет равен 0, если всё принадлежит одному человеку, то — 1). Выполним "двумерный" анализ сначала для сырых данных, затем для нормализованных.

Рис. 3.23 Диаграмма рассеяния для пары переменных Общая преступность - Индекс Джини: а) сырые данные, b) нормализованные

Как можно видеть статистика подтверждает хорошо известную истину: реальность всегда несколько сложнее нашего представления о ней. Так, на графике Общая преступность|Индекс Джини (Рис. 3.23 a) высокие значения преступности (выше 10 тысяч на квартал за период в 15 лет) соответствуют умеренно высокие (0,4 - 0,6) значения Неравенства доходов, однако общая тенденцию уловить весьма затруднительно. На Диаграмме рассеяния нормализованных значений плотное "облако" значений вытянуто вдоль оси зависимой переменной Y и имеет заметный наклон, подтверждающий увеличение Общей преступности при росте Индекса Джини (т.е., фактически - при росте неравенства доходов).

Проверим, подтверждают ли излюбленную социальными психологами и бихевиористами теорию о социально обусловленности преступности другие не менее важные экономические показатели, например - Годовой доход домохозяйств и Уровень безработицы.

Рис. 3.24 Диаграмма рассеяния для переменных: а) Общая преступность - Годовой доход домохозяйств (сырые данные), b) Общая преступность - Уровень безработицы (нормализованное значение)

Огромный объем значений (т.е., зафиксированных за 15 лет преступлений), дает "пухлое" облако с ореолом выбросов, но если провести кривую через центр плотности облака она покажет резкое падение числа преступлений за пределами объема годового дохода в 100 000 $ (Рис. 3.24 a). Уровень безработицы образует более сложное и расширенное кверху скопление значений (Рис. 3.24 b), но и здесь можно отметить заметный наклон вправо - в сторону возрастания числа безработных.

Отличная возможность получения Диаграмм рассеяния с построением кривой тренда предоставляется в SAGA GIS. По клику правой кнопкой мыши на слое во вкладке Data переходим в Attributes и далее имеем выбор: построение Диаграммы для одной переменной или Диаграмма рассеяния для двумерного анализа. Соответственно Data = NYCTRACTs >> RC >> Attribute >> Diagram - в открывающемся диалоговом окне Properties выбираются переменная, тип диаграммы (точечная, столбчатая, линейная). Результирующую диаграмму можно настраивать повторно через вкладку Properties.

Рис. 3.25 Диаграмма рассеяния для единственной переменной (Общее Число Преступлений) в SAGA GIS

Аналогично строится Диаграмма рассеяния для двух переменных: Data = NYCTRACTs >> RC >> Attribute >> Scatterplot. В открывающемся окне кроме выбора двух переменных (X, Y) предоставляется возможность выбора формулы предполагаемой регрессии; по умолчанию:
Regression Formula Y = a + b * x.

На листе Диаграмма рассеяния мы видим не просто линию, отражающую линейную регрессию (как вариант линейной зависимости), но и соответствующие коэффициенты, которые могут быть скопированы в настройках Options >> Regression Details.

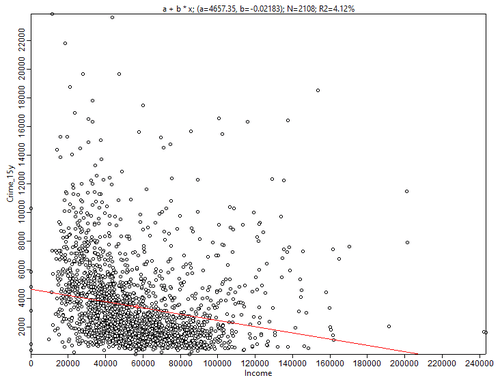
Рис. 3.26 Диаграмма рассеяния для двух переменных (Общее Число Преступлений и Годовой доход домохозяйств) в SAGA GIS, Regression Details a + b * x; a = 4657.35; b = -0.02183; N = 2108; R2 = 4.11778

Следует иметь ввиду, что в записи формулы линейной регрессии, используемой в SAGA GIS Regression Formula Y = a + b * x, b - это множитель независимой (факторной) переменной x, который определяет наклон линии slope, а b - константа intercept, определяющая место пересечения прямой с осью координат. N - число наблюдений (в данном случае число кварталов Нью-Йорка. Положительный наклон линии тренда означает положительную связь (рост предиктора X влечет за собой рост зависимой переменной Y, отрицательный наклон отражает отрицательную связь (рост предиктора X сопровождается уменьшением зависимой переменной Y.

Проверим два других с помощью SAGA GIS два других достаточно распространенных "бытовых" предположения: первое связывает преступность с уровнем образования, второе - с долей афроамериканского населения. Регрессионная кривая на Диаграмме рассеяния позволят эксперту оценить (в первом приближении) насколько модель линейной регрессии вообще пригодна для описания взаимосвязи между двумя переменными; не менее полезен в этом смысле и коэффициент детерминации R², показывающий нам сколько процентов дисперсии зависимой переменной (в данном случае - числа преступлений) может быть объяснено предиктором X.

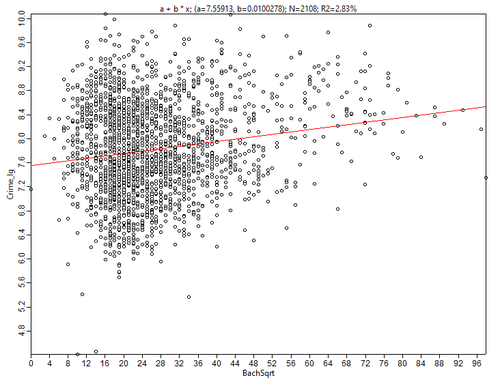
Рис. 3.27 Диаграмма рассеяния для переменных Общая преступность - Число бакалавров; Regression Details: a + b * x; a = 7.55913; b = 0.0100278; N = 2108; R2 = 2.83129

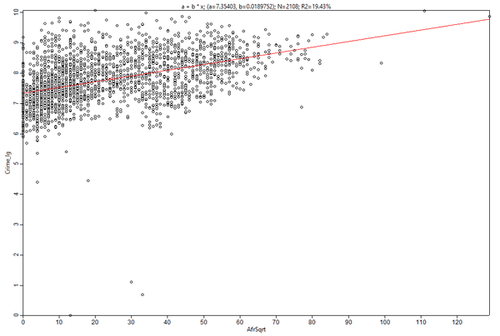
Рис. 3.28 Диаграмма рассеяния для переменных Общая преступность - Доля афроамериканцев в общей численности населения квартала; Regression Details a + b * x; a = 7.35403; b = 0.0189532; N = 2108; R2 = 19.43

Очевидно, что несмотря на внешне похожие Диаграмма рассеяния "облако точек" для пары Преступность-Бакалавры имеет более "рыхлую" структуру - разброс значений здесь больше и очень невелик процент "объясненной" зависимости (2,8%), в то время как для пары Преступность - Афро-американцы мы имеем статистически значимую величину 19,4%.

Таким образом, уровень бедности, безработица, уровень образования и расовый состав если и связаны с преступностью, то непростыми и скорее всего - нелинейными причинно-следственными зависимостями. Сколь бы не был велик соблазн "ухватиться" за объяснение, на данном этапе моделирования его следует преодолевать, ибо задача ESDA несколько иная: отобрать перспективные факторные переменные для объяснения изучаемого феномена.

В процессе подобного поиска мы можем "примерить" разные переменные-факторы. Посмотрим, насколько принципиально отличаются парные (двумерные) диаграммы для другой зависимой переменной - Онкологических заболеваний. Для начала построим хороплет для этой переменной

Картограмма онкологических заболеваний (2005-2009 гг.) обнаруживает все признаки пространственной неоднородности, но, по крайней мере на первый взгляд, не имеет признаков внутренней структуры (т.е., наличия кластеров или какого-либо регулярного распределения).

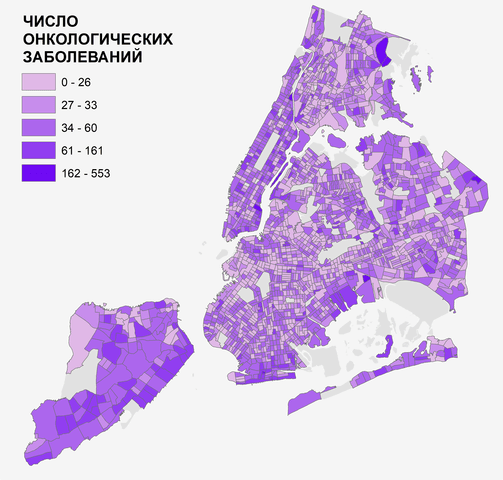
Рис. 3.29 Хороплет подтвержденных случаев онкологических заболеваний по кварталам Нью-Йорка за 4 года

Рис. 3.30 a) Гистограмма распределения и b) QQ-график онкологических заболеваний

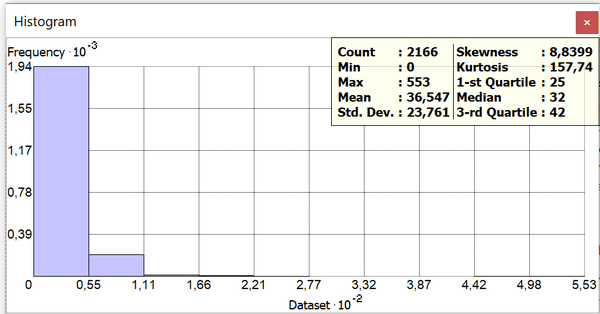
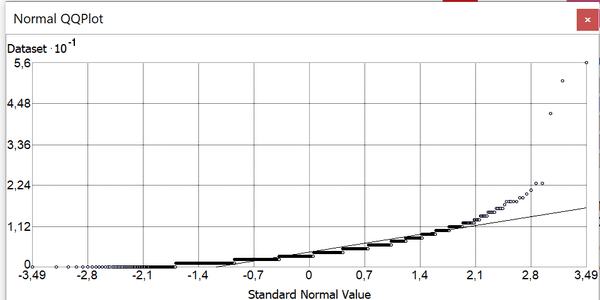
Гистограмма также близка к "паретианскому" распределению, в котором, среднее больше чем медиана, существует значительная асимметрия (8,8) влево в область меньших значений и положительные эксцессы (157,7) с "тяжелым" хвостом; очевидно также, что кривая на QQ-графике почти не совпадает с прямой линейной функции, приближаясь к ней только в области средних значений.

Попытаемся "примерить" к феномену заболеваемости объясняющие социальные факторы.

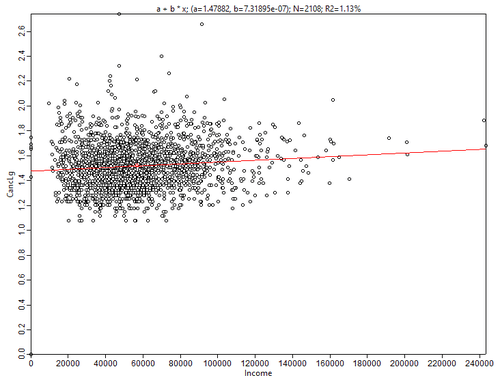
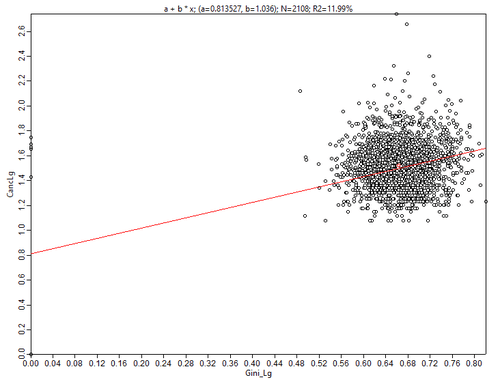
Рис. 3.31 Диаграммы рассеяния для переменной Общее число онкозаболеваний в последовательных парах: а) Доход домохозяйств, b) Индекс неравенства доходов Джини

О чем говорят эти диаграммы? Распределение заболеваний обнаруживает довольно высокую "компактность" значений со сравнительно небольшим (относительно общего объема значений) числом выбросов. Однако объясняющая функция Дохода Домохозяйства чуть более одного процента, в то время как Индекс Джини "объясняет" 11% наблюдений.

У заболеваемости могут быть разные причины, в том числе - генетические, следовательно небессмысленным является вопрос о том, одинаково ли часто болеют представители белого и афроамериканского населения?

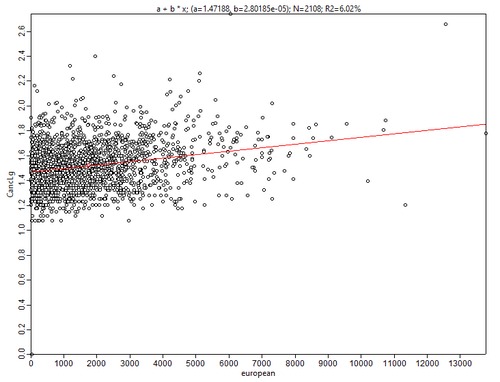
Рис. 3.32 Диаграммы рассеяния для переменной Общее число онкозаболеваний в последовательных парах: а) Заболеваемость - Численность афроамериканцев, b) Заболеваемость - Численность белых американцев

Две построенные диаграммы на самом деле демонстрируют интересную закономерность: увеличение доли афроамериканского населения явно работает против роста переменной Число онкологических заболеваний (да и коэффициент детерминации здесь выше - 6%).

Велик соблазн связать заболеваемость с комфортностью среды - например, с объемной плотностью застроенности кварталов и площадью элементов зеленой инфраструктуры.

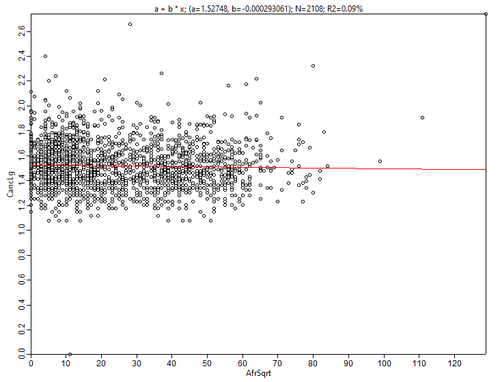
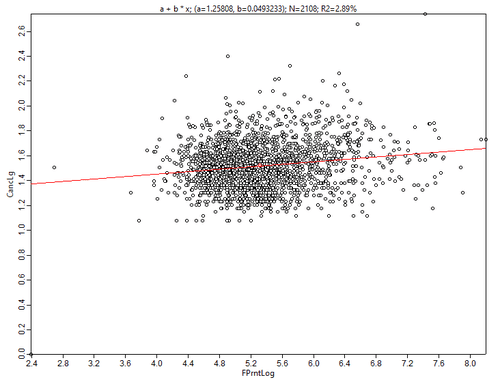
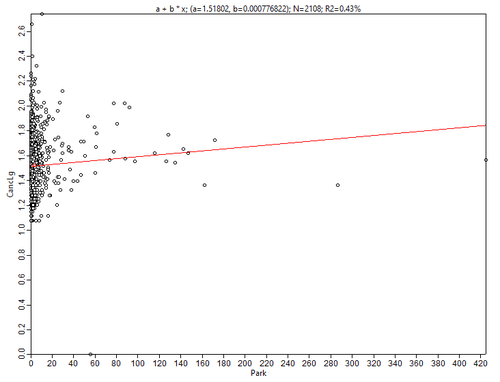
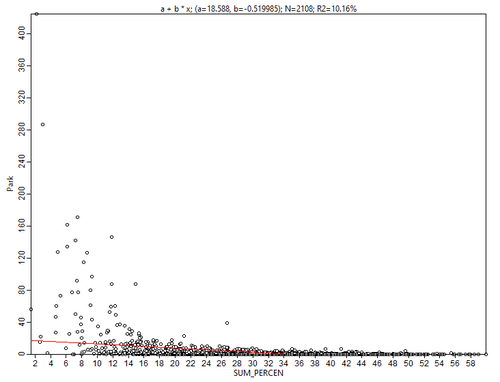
Рис. 3.33 Диаграммы рассеяния для переменной Общее число онкозаболеваний в последовательных парах: а) Заболеваемость - Плотность застройки FootPrint, b) Заболеваемость - Площадь парков

Однако, построенные диаграммы не свидетельствуют о наличии какой-либо надежной связи между заболеваемостью и факторами комфортности среды. Имеет смысл проверить на наличие корреляции и некоторые пары переменных-предикторов будущей модели. Например, зависимость обнаруживают предсказуемо связанные пары Общая площадь парков - Плотность застройки, или Доля бакалавров - Доля афроамериканцев.

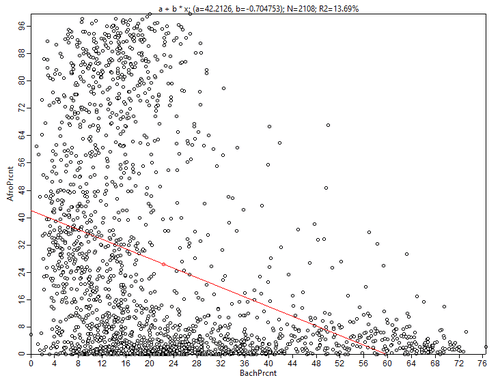
Рис. 3.34 Диаграммы рассеяния для переменных: а) Общая площадь парков - Плотность застройки (горизонтальный FootPrint без учета высоты зданий), b) Доля бакалавров - Доля афроамериканцев в общей численности населения квартала

Тем не менее, связь в обоих случая хоть и наблюдается, но объясняет не такой уж большой процент выборки - 10% в паре Общая площадь парков - Плотность застройки" и 12% в парке Бакалавры - Афроамериканцы.

Таким образом, парные Диаграмма рассеяния весьма ограниченно пригодны для построения серьезных гипотез и выработки заслуживающих доверия объяснений. Кроме того, если проверку на пригодность для включения в модель необходимо осуществить для большого числа переменных составление отдельных диаграмм для каждой пары может оказаться трудоемким занятием. В этом смысле "прорывным" решением является построение Матрицы точечной диаграммы, которая отображает парные отношения сразу между всеми привлеченными к анализу переменными.

В ArcMAP 10.x Main Menu >> View >> Graphs >> Create Scatter plot Matrix Graph) >> Layer = NYCTRACTs. Далее указываются переменные (зависимая и предикторы).

Рис. 3.35 Матрица точечной диаграммы для пяти переменных: Общая преступность (Crime), Годовой доход домохозяйства (Income), Число людей со степенью бакалавра (Bachel), Число безработных афроамериканцев (Afrounempl), Общее число онкологических заболеваний (Cancer), Градостроительная нагрузка (FootPrint)

Матрица точечной диаграммы позволяет оценить потенциальную (парную) взаимозависимость между любым числом переменных, при этом для каждой пары признаков выстраивается точечная диаграмма, а для каждой отдельной переменной - гистограмма. Таким образом эта утилита заменяет сразу два действия (правда, мы не увидим здесь рассчитанные базовых статистик) и хорошо подходит для "разведочных" действий по выявлению зависимостей.

Диаграмма для каждой пары может быть увеличена: щелчок инструментом Выбор|Select Features помещает увеличенную копию в верхний правый угол листа. Матрица как и все другие построенные в этом разделе графики и диаграммы могут быть сохранены в любом графическом формате по правой кнопке мыши RC >> Save в формате Графический Файл Graf File - grf или экспортированы в любой предпочитаемый формат RC >> Export (Рис. 3.35). Таким образом, Матрица точечной диаграммы - удобный инструмент Исследовательского Анализа Данных (ESDA), позволяющий сделать первые предположения о характере возможных зависимостей и отобрать переменные-кандидаты для более глубокого изучения..

Изучая зависимость между переменными с помощью Диаграмм рассеяния в рамках Исследовательского Анализа, мы можем получить один из нижеследующих результатов:

Отсутствие корреляции (независимые переменные): распределение на диаграмме выглядит как округлое (часто - "рыхлое") облако без возможности провести хоть какую-то обобщающую ось;
Линейной корреляции нет, но через облако данных можно провести обобщающую кривую, в этом случае можно либо использовать нелинейную модель, либо преобразовать данные;
Линейной корреляции нет, но в данных наблюдается закономерность, которая (как вариант) может быть отражена параболической кривой, проходящей через точки;
Положительная корреляция, когда точки или их уплотнения пересекаются направленной в верхний правый угол диаграммы прямой линией;
Отрицательная корреляция точки или их уплотнения пересекаются направленной в нижний правый угол диаграммы прямой линией.

Как показывают приведенные выше примеры, Точечные Диаграмма рассеяния - это ответ на вопрос о существовании линейной корреляции между переменными. Коэффициент детерминации для линейной регрессии равен квадрату коэффициента корреляции. Следовательно, с помощью Диаграмм рассеяния мы можем определить:

характер связи (положительная отрицательная - определяется наклоном прямой),
силу связи (определяется по коэффициент корреляции - его можно получить из коэффициента детерминации),
объем выборки (в %) объясняемый обнаруженной корреляцией.