I. ОСНОВЫ ПРОСТРАНСТВЕННОГО АНАЛИЗА 6. РЕГРЕССИОННЫЙ АНАЛИЗ: ЛИНЕЙНАЯ И ГЕОГРАФИЧЕСКИ ВЗВЕШЕННАЯ РЕГРЕССИЯ 6.1. Регрессионный анализ: последовательность действий 6.2. Анализ Главных Компонент для выбора переменных 6.3. Исследовательская регрессия 6.4. OLS - Метод наименьших квадратов 6.5. Географически взвешенная регрессия

I. ОСНОВЫ ПРОСТРАНСТВЕННОГО АНАЛИЗА

6. РЕГРЕССИОННЫЙ АНАЛИЗ И ГЕОГРАФИЧЕСКИ ВЗВЕШЕННАЯ РЕГРЕССИЯ

6.1. Регрессионный анализ: последовательность действий

Регрессионный анализ - это способ выявления взаимосвязей между зависимой переменной и гипотетическими факторами, определяющими ее значение (состояние), которые в данной модели могут считаться независимыми объясняющими переменными. После того, как мы подвергли наши данные о преступности в Нью-Йорке различным видам "испытаний" (отображение, выведение центрографических показателей, выяснение особенностей пространственного распределения и определение наличия и знака пространственной автокорреляции) можно приступить к собственно поиску причинно-следственных связей, точнее, к их доказательству, поскольку отдельные аспекты зависимости между исследуемым феноменом и некоторыми переменными мы (отчасти) обнаружили в результате предшествующего анализа.

Последовательность такого рода моделирования причинно-следственных связей может выстраиваться различным образом - в зависимости от характера данных и поставленных задач. Более-менее обычная традиция диктует следующий порядок действий:

  1. Построение общей гипотезы исследования с выбором "предикторов" для модели;
  2. Проверка переменных на коллинеарность, а модели в целом - на "переоснащение";
  3. Проверка набора данных на наличие пропущенных значений;
  4. Проверка набора данных на наличие выбросов значений, которые могут существенно исказить общую картину;
  5. Проверка модели на необходимость включения "фиктивной" переменной;
  6. Стандартизация и/или нормализация данных;
  7. Выбор вида регрессионного анализа;
  8. Осуществление Исследовательской Регрессии;
  9. Интерпретация коэффициентов регрессии;
  10. Перебор и выбраковка первичного набора объясняющих переменных;
  11. Дополнительная диагностика посредством Метода Наименьших Квадратов (OLS);
  12. Применение Географически Взвешенной Регрессии (GWR) для обработки пространственной неоднородности.

Рассмотрим перечисленные шаги исследования более подробно.

На этапе Построение общей гипотезы исследования мы должны изложить максимально ясным образом свое представление о том, какие факторы могут влиять на состояние и поведение зависимой переменной. Хорошее подспорье для таких построений - так называемые "ментальные карты", для разработки которых существует сегодня разнообразное программное обеспечение (например, Microsoft Visio), впрочем, вполне можно обойтись и рисованием обычных блок-схем карандашом на листе бумаги.



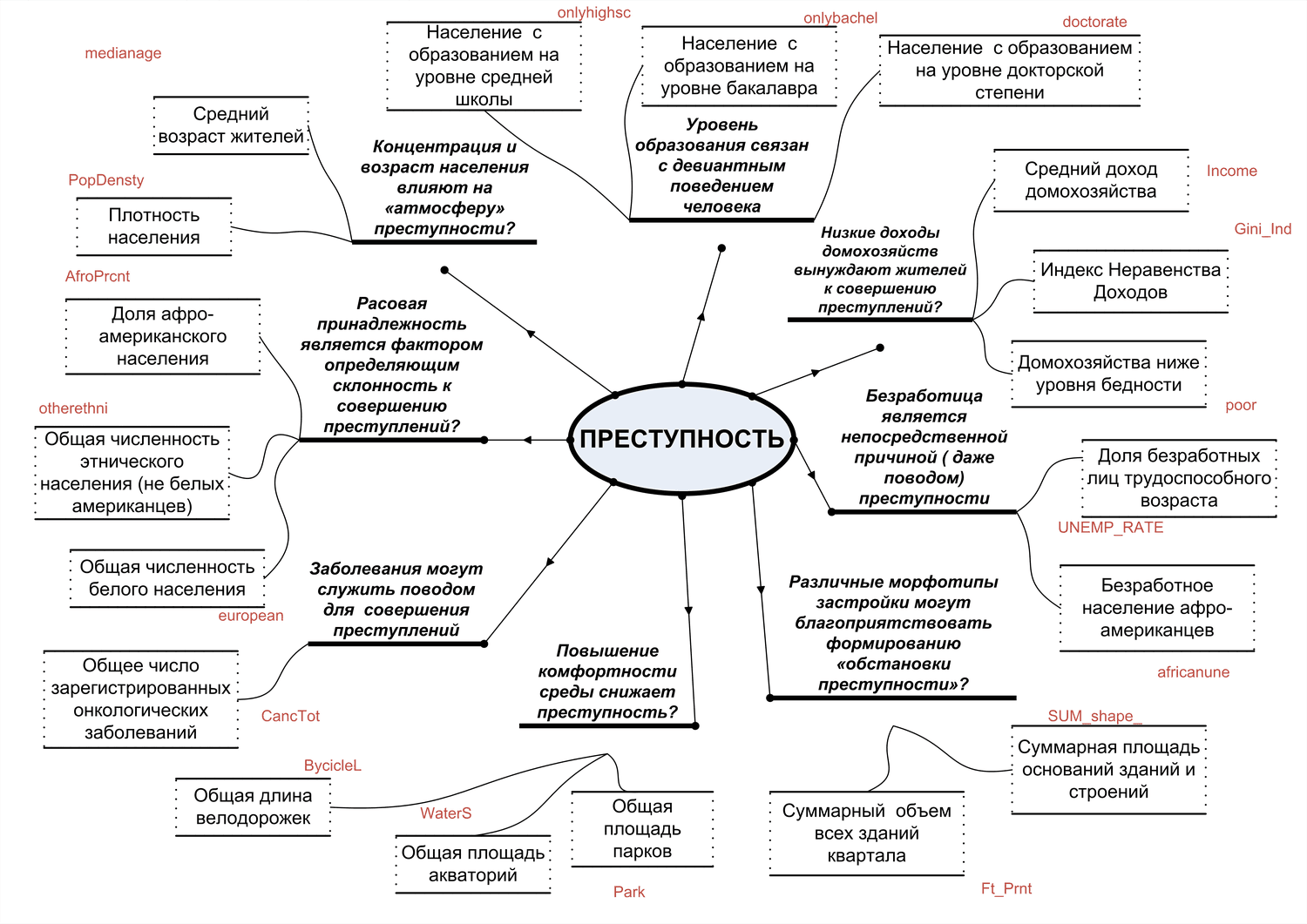
Рис. 6.1 Ментальная "карта" гипотезы факторов совершения тяжких преступлений против личности в Нью-Йорке

На схеме Рис. 6.1 представлена гипотеза причинно-следственной связи для феномена "убийства" в Нью-Йорке (с опорой на имеющиеся и некоторые добавленные сведения). Разумеется - мы не являемся экспертами в данном вопросе и можем полагаться лишь на литературные данные [Grana, Windell, 2017] и собственную интуицию. Исходя из наличных данных мы сделали следующие предположения (это именно предположения, лишенные пока какой-либо доказательной базы):

  1. Расовая принадлежность, возможно, является фактором, определяющим сравнительно большую или меньшую склонность к совершению преступлений;
  2. Концентрация и возраст населения влияют на «атмосферу» преступности;
  3. Вполне вероятно, что уровень образования в какой-то степени определяет девиантное поведение человека;
  4. Низкие доходы домохозяйств вынуждают жителей к совершению преступлений;
  5. Безработица является непосредственной причиной (даже поводом) преступности;
  6. Различные морфотипы застройки могут благоприятствовать формированию «обстановки преступности»;
  7. Повышение комфортности среды снижает преступность;
  8. Заболевания могут служить поводом для совершения преступлений.

Таким образом, в нашей гипотезе 8 потенциальных причин, каждая из которых может быть выражена двумя-тремя переменными. Например, интуитивно мы понимаем, что бедность может влиять на совершение преступлений, но понятие "бедность" в свою очередь описывается разными параметрами: общий уровень доходов (как самый общий показатель достатка/бедности), некий нижний уровень доходов (как показатель действительной нищеты) или, наконец, выраженное неравенство доходов (как возможная причина зависти и мотивации к совершению преступления). Какой из этих параметров находится в наиболее тесной связи с зависимой переменной - заранее определить невозможно.

Проверка модели на "переоснащение". Изложенный выше пример с различными параметрами бедности хорошо объясняет "соблазн" привлечения большого количества переменных: проще говоря, если вы имеете системное представление о феномене вам (естественно!) хочется "затащить" в модель все известные предикторы (ведь каждый из них предположительно своеобразно влияет на зависимую переменную). Однако подобное решение не безобидно в силу возможной коллинеарности показателей, которые могут параллельно и однообразно изменяться в пространстве, что приведет к эффекту "переоснащения модели|model overfitting". Мультиколлинеарность существует между двумя или более переменными в наборе данных, когда они сильно коррелированы между собой, поэтому привлечение многих переменных, описывающих схожие (близкие) свойства изучаемого феномена, не обязательно приводит к созданию лучшей модели.

Проверка переменных на коллинеарность может быть осуществлена разными способами. Можно сравнивать привлеченные факторы попарно, используя приемы Двумерного статистического анализа - Диаграммы рассеяния, либо выстраивая Матрицы точечных диаграмм для многих переменных одновременно. В многомерном анализе чаще используют Principal Component Analysis|Анализ главных компонент - метод, который уменьшает число факторов до набора не связанных (или почти несвязанных) переменных, называемых основными компонентами, чтобы, с одной стороны, упростить интерпретацию, с другой - сохранить большую часть потенциально полезной информации.

Опыт геоинформационного моделирования свидетельствует, что, переоснащение чаще всего происходит, при нарушенном соотношении числа переменных и количества наблюдений, иными словами, если у нас, скажем, 12 случаев заболеваний (изучаемый феномен), то не имеет смысла привлекать 20 переменных для объяснения. Предлагается [de Vaus, 2002; Tabachnick et al., 2012] следовать простым правилам, помогающим избежать перегрузки модели переменными:

  1. При использовании множественной линейной регрессии отношение наблюдений к переменным должно быть больше 20 / 1;
  2. Размер выборки должен быть не менее 100 + k, где k - количество независимых переменных (факторов);
  3. В случае ненормально распределенной зависимой переменной, выборки должны быть еще увеличены.

Эти эмпирические правила предназначены для общего руководства. Окончательное решение о выборе переменных должно приниматься в зависимости от рассматриваемой проблемы и имеющихся данных. Корректный подход заключается в том, чтобы изначально построить простую модель, объясняющую большую долю вариаций, а затем добавлять, менять или убирать переменные, добиваясь лучшего результата.

Недостающие значения. До первого запуска регрессионного анализа следует проверить существуют ли недостающие значения: в рассматриваемом случае с кварталами Нью-Йорка — это кварталы, не несущие значений исследуемого явления (показателей преступности) и/или значений независимой переменной. Тремя наиболее распространенными способами устранения пропущенных значений являются:

  1. Удаление наблюдений, содержащих пропущенные значения;
  2. Замена пропущенных значений переменной средним значением этой конкретной переменной;
  3. Заполнение пропущенных значений интерполяцией, например - с помощью простой линейной регрессии.

В нашем случае нежилые кварталы Нью-Йорка, например - парковые территории - не содержат данных о доходах домохозяйств или образовательном уровне населения, и хотя само изучаемое явление (преступность) на них "проецируется" - поскольку преступления (пусть и редкие) там все же зафиксированы, но в рамках данной модели корректнее исключить их из анализа.

Проверка набора данных на наличие выбросов и Точек чрезмерного влияния|Leverage Points - также необходимый этап анализа. Свои выбросы может иметь любая из независимых переменных, привлеченных к анализу: если выбросы единичны в этом нет большой угрозы для моделирования. Хуже если выбросов много и гораздо хуже если выбросы двух или более переменных образуют общее скопление в пространстве ординации, что возможно, если переменные хотя бы частично взаимозависимы или имеют схожую пространственную автокорреляцию. В регрессионном анализе существует три подхода для обработки таких наблюдений:

  1. Фиксация и удаление выбросов с помощью Анализа Кластеров и Выбросов до проведения регрессионного анализа;
  2. Выполнение Множественной Линейной Регрессии (MLR), с включением всех данных, и созданием стандартизированного графика остатков, на котором можно проследить как выбросы, так и точки с чрезмерным влиянием. После удаления и тех и других можно снова протестировать модель - если результаты будут улучшены, следует отказаться от наблюдений, содержащих выбросы и точки чрезмерного влияния;
  3. Применение так называемой "робастной регрессии" - одного из приемов "надежной статистики".

Включение фиктивной переменной. Фиктивная переменная|Dummy Variable это двоичная переменная, получающая значения 1 или 0, указывающие на наличие (1) или отсутствие (0) некоторого категориального эффекта. Целесообразность ее введения определяется гипотезой: например, если бы у нас были данные по гендерному составу лиц, совершающих преступления, то, возможно, имело бы смысл ввести эту переменную в модель: вполне вероятно, что убийства совершают не просто люди с низкими доходами и невысоким образовательным цензом, но, как правило, мужчины, следовательно, число именно таких лиц в квартале является значимым сочетанием обстоятельств. Такая переменная вводится как категориальная, например 0 - женский пол, 1 - мужской (или наоборот).


6.2. Анализ Главных Компонент для выбора переменных

Многомерные данные — это данные с более чем двумя значениями, записанными для каждого наблюдения [O'Sullivan, Unwin, 2010, p.316]. Типичное представление многомерного набора данных A с n наблюдениями и p переменными осуществляется через матрицу, в которой столбцы представляют p переменных, а строки представляют n наблюдений. Многомерные данные существуют в многомерном пространстве, где число измерений равно числу переменных. Например, область тематического исследования с 2108 жилыми кварталами Нью-Йорка и 20 переменными представляет собой p=20 двадцатимерный набор данных, состоящий из n=2108 наблюдений.

Анализ Главных Компонент|Principal Component Analysis (PCA) — это метод, используемый для обобщения многомерных данных в меньшем количестве интерпретируемых переменных. PCA уменьшает размеры многомерного набора данных до набора независимых некоррелированных переменных, называемых главными или основными компонентами, чтобы сделать анализ более полным и упростить интерпретацию, в то же время сохраняя большую часть информации (вариаций), существующей в наборе данных. <Основной компонент представляет собой линейную комбинацию исходных (или стандартизированных) значений переменных и рассчитывается путем извлечения собственных векторов и собственных значений матрицы дисперсии–ковариации или корреляционной матрицы.

Собственные векторы интерпретации извлекаются из матрицы дисперсии–ковариации и используются для построения новых осей, называемых главными компонентами, которые соответствуют направлению (в исходном пространстве) с наибольшей дисперсией данных [Hamilton, 2014].

Чтобы лучше понять, как работает алгоритм Анализ Главных Компонент, рассмотрим конкретный пример. Предположим, мы исследуем с помощью линейной регрессии взаимосвязь между тяжкими преступлениями и долей афроамериканского населения в кварталах Нью-Йорка. Используя точечную диаграмму двумерного пространства, построенную в SAGA GIS, мы получаем прямую линейной регрессии и формулу типа y: a + b * x для 2108 кварталов (N):

y: 7.36 + 0.019 * x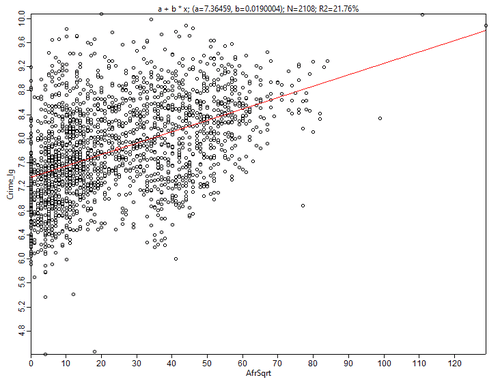


Рис. 6.2 Диаграмма рассеяния для переменных Общая преступность - Доля афроамериканцев в общей численности населения квартала

Мы можем рассчитать дисперсию σ2 в направлении X и дисперсию σ2 в направлении Y в качестве меры разброса значений. Тем не менее, горизонтальная и вертикальная дисперсия не совсем точно объясняет четкую диагональную тенденцию. Вместо вычисления дисперсии для осей X и Y лучше повернуть их так, чтобы ось x фиксировала максимальную дисперсию облака точек данных. Ось Y останется ортогональной к X, захватывая другую долю дисперсии. Новые оси являются первым и вторым основными компонентами, и, одновременно, это оси Standard Deviational Ellipse|Эллипса стандартного отклонения - одной из центрографических дистанционных характеристик распределения.



Рис. 6.3 Эллипсы стандартного отклонения для точек преступлений, совершенных афро-американцами (три эллипса соответствуют стандартному отклонению первого, второго и третьего порядков, охватывающих соответственно 68%, 95% и 99% точек)

Центр эллипса — это средний центр точек данных. Главная ось лежит на первом компоненте, а второстепенная ось, которая ортогональна главной, лежит на втором компоненте. Длина каждой оси равна квадратному корню из соответствующего собственного значения. Угол поворота эллипса (указан в таблице слоя как Rotation) и будет углом разворота ортогональных осей.

В ArcMAP10.x для того, чтобы использовать Principal Component Analysis (PCA) набора Multivariate группы Spatial Analyst Tools необходимо создать из векторного файла полигонов (кварталы Нью-Йорка) серию растров для каждой отдельной переменной и загрузить их потом в качестве растровых каналов (raster bands) генерируемого инструментом многоканального растра.

До проведения PCA целесообразно еще раз убедиться в отсутствии резких различий в диапазонах переменных, и провести (если необходимо) нормализацию или шкалирование данных (Таблица 6.1).

Таблица 6.1 Трансформация данных, используемая для уменьшения асимметрии и нормализации данных
№ Наименование растра Содержание
переменной		 Преобразование исходного
значения
1 poorsqrt доля домохозяйств ниже уровня бедности нормализация
2 giniIndex индекс Джини нормализация
3 afrunmploysrt доля афроамериканского безработного населения нормализация
4 income среднегодовой доход домохозяйств шкалирование
5 unemploy уровень безработицы нормализация
6 bachprcnt доля лиц со степенью бакалавра -
7 medianage средний возраст населения -
8 popdnslg плотность населения нормализация
9 footprint объемный след застройки шкалирование
10 parcprcnt доля парковых территорий -
11 cancersqroot число онкологических диагнозов нормализация

Следует иметь ввиду, что при загрузке растров в диалоговом окне PCA input raster bands - вне зависимости от того, как вы это делаете - по одному или списком, захватив их в таблице слоев Table of Content - вверху списка окажутся слои, загруженные последними и скрипт пронумерует их именно в этой последовательности; это важно, потому что в выходных таблицах алгоритма PCA значатся номера слоев (но не их названия).

На выходе PCA - многоканальный растр и файл отчета в формате txt, открывающийся обычным образом: Result >> RCM >> Output Data File: PCA.TXT. Этот файл содержит пять разделов:

Input raster(s) - отображает последовательность загрузки - верхний растр получает номер 1, нижний - последний номер (в нашем случае - 19)
COVARIANCE MATRIX - матрица ковариации, является обобщением дисперсии (диагональные элементы ковариационной матрицы показывают дисперсии по изначальному базису, а ее собственные значения – по новому);
CORRELATION MATRIX - матрица корреляции;
EIGENVALUES AND EIGENVECTORS - айгензначения и значения айгенвекторов,
PERCENT AND ACCUMULATIVE EIGENVALUES - процент объясненной вариабельности.

Для удобной работы с выводными данными PCA лучше скопировать таблицы каждого раздела в Excel, использовав при необходимости прием разделение данных по столбцам и не забывая преобразовать формат ячеек в "числовой". После первого прогона инструмента необходимо зафиксировать "лишние" переменные, получившие высокий коэффициент в Матрице корреляции. Для лучшей ориентировки можно заменить номера переменных названием исходных растров (если забыли порядок загрузки - смотрим в первых раздела TXT-отчета Input raster).


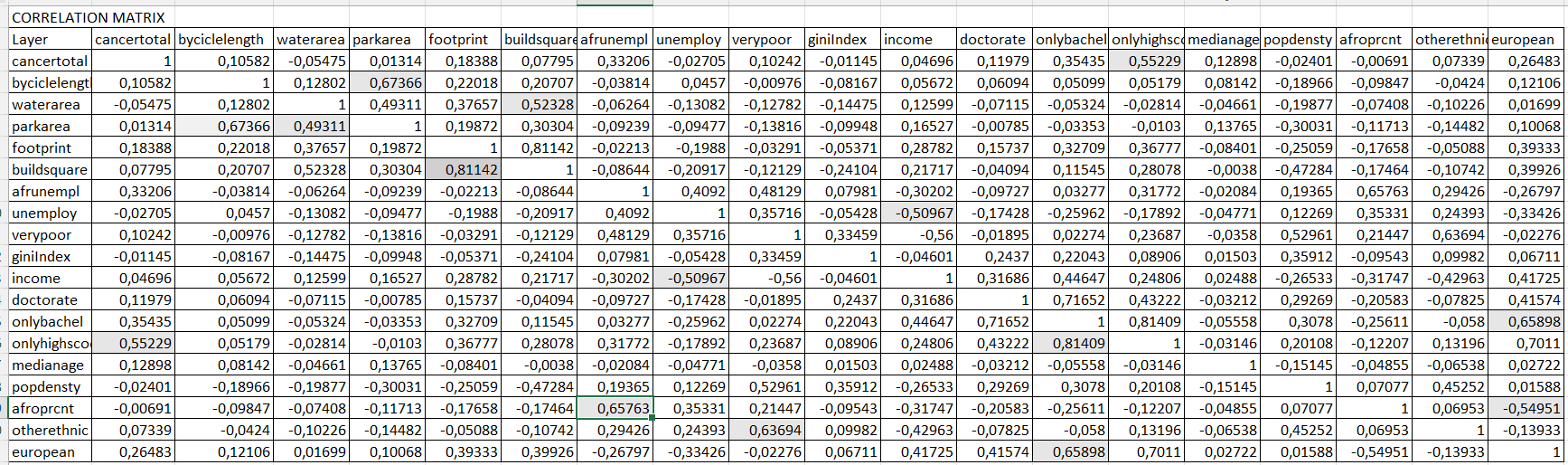
Рис. 6.4 Матрица корреляции Анализа Главных Компонент для 19 переменных (импортирована в Excel, ячейки с высокими коэффициентами корреляции затенены)

Далее ищем пары с высоким > 0,8 и значительным > 0,5 коэффициентом корреляции (в нашем случае они вполне ожидаемы и объяснимы):

  • buildsquare (площадь занимаемая суммой оснований зданий и сооружений) и footprint (объемный индекс застроенности, совокупная площадь с учетом этажности);
  • onlyhighscool (лица со школьным образованием) и onlybachel (лица со степенью бакалавра);
  • onlybachel (лица со степенью бакалавра) и doctorate (лица со степенью PhD);
  • afroprcnt (доля афроамериканского населения) и afrunempl (доля безработного афроамериканского населения);
  • otherethnic (доля иных этносов, т.е., не белого и не афроамериканского населения) и verypoor (процент беднейших домохозяйств);
  • european (доля европейского населения) и onlybachel (лица со степенью бакалавра);
  • byciclelength (длина велосипедных дорожек) и parkarea (площадь парков) waterarea (лощадь акваторий) и parkarea (площадь парков).

Таким образом модель явно переоснащена и можно без ущерба для корректности избавиться от восьми переменных, выбирая из пары связанных "лучшие" (с большим коэффициентом детерминации на парных графиках с зависимой переменной - преступностью) переменные. В качестве показателя застроенности оставляем объемный индекс, (учитывающий и высоту зданий) и убираем площадь оснований зданий и сооружений; в группе, характеризующей уровень образования избавляемся от школьной ступени и от доктората; выбираем как более точную переменную безработного афроамериканского населения (избавляемся от доли афроамериканского населения), также убираем еще один этнический признак - otherethnic|иные этносы, т.к., он косвенно отражается в показателе verypoor|беднейшие домохозяйства, также убираем и долю белого населения, ибо оно достаточно жестко связано с долей лиц с бакалаврским дипломом. Все три показателя комфортности среды оказались тесно связанными, поэтому целесообразно избавиться от длины велодорожек и площади акваторий, которая зависит от площади парков.

Следующий запуск алгоритма PCA проводим для сокращенного списка из 11 переменных, загружая их в порядке предварительного представления об их значимости. Полученная для 11 переменных Матрица Корреляции, с одной стороны, уже свободна от связанных между собой пар факторов, с другой - содержит не ничтожные коэффициенты (значение R2 около +0,3 или - 0,3): обстоятельство, сохраняющее перспективы для поиска значимых связей между зависимой переменной и предикторами.



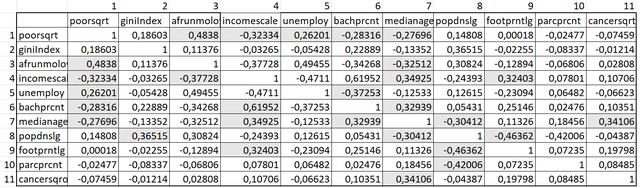
Рис. 6.5 Матрица корреляции Анализа Главных Компонент для 11 переменных (затенены ячейки с "перспективными" для регрессионного анализа значениями)

Следует обратить внимание и на другие разделы отчета PCA-анализа, содержащиеся в TXT-файле. Первый раздел отчета - Матрица Ковариации - содержит величину дисперсии признаков по диагонали (дисперсия одномерной величины), а в остальных ячейках – ковариации соответствующих пар признаков (ковариации двух признаков); в силу симметричности ковариации матрица тоже будет симметрична.



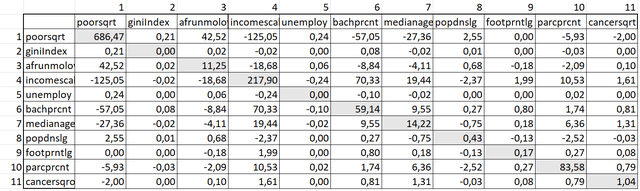
Рис. 6.6 Матрица ковариации Анализа Главных Компонент для 11 переменных (затенены диагональные ячейки с величиной дисперсии для каждой переменной)

По Матрице ковариации можно выделить переменные с большим значением дисперсии - в нашем случае это Домохозяйства ниже уровня бедности, Средний доход домохозяйств, Удельная площадь парковых территорий.

Третий раздел TXT-отчета PCA-анализа хранит айгенпары - Собственные Вектора|Eigenvectors и Айгензначения|Eigenvalues. Айгенвекторы совпадают с эллипсом радиусом в две сигмы, т.е., содержат в себе 95% всех наблюдений.



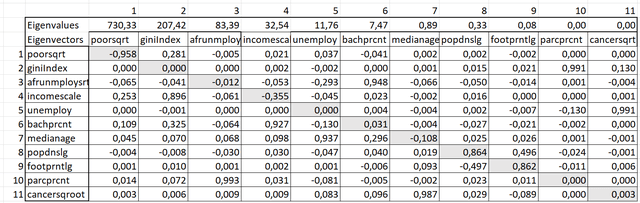
Рис. 6.7 Скриншот Таблицы Собственные векторы (затененные ячейки диагонали) и парные Айгенвекторы для 11 переменных

Айгензначения и Айгенвекторы должны служить ориентиром для решения основного вопроса - выбора переменных, которые будут задействованы в последующем регрессионном анализе. Чем больше собственное значение Eigenvalue, тем более значимым является компонент, поскольку он отражает большую часть изменчивости исходных данных. Как можно видеть по таблице (Рис. 6.7) в данном случае высокие айгензначения характерны для первых шести компонентов (Число хозяйств ниже уровня бедности, Индекс Джини, Число безработных афроамериканцев, Общий уровень безработицы, Доля лиц со степенью бакалавра). Можем ли мы отбросить остальные переменные?

Ответ на этот вопрос не так прост. Поскольку каждое собственное айгензначение представляет дисперсию связанного ряда оценок основных компонентов, целесообразно сохранить наименьшее количество основных компонентов, которые объясняют желаемую долю общей дисперсии. Именно так - с меньшим количеством измерений возможно охватить большую часть изменчивости и информации в данном наборе данных. Существует множество различных способов определения количества значимых компонентов, которые необходимо сохранить, три наиболее используемых метода на практике включают:

  1. Правило "предельно низкой величины айгензначения",
  2. Совокупный (накопленный) процент от общей дисперсии,
  3. Построение Scree-графика.

Правила предельно низкой величины айгензначения введены разными исследователями в качестве ориентировочных рекомендуемых пороговых величин eigenvalues|айгензначения. Так, правило Кайзера, предусматривает сохранение только одной главной переменной из числа тех, чье айгензначение не превышает 1,0. Аналогичное правило Джоллифа [Jolliffe, 2002], устанавливает пороговое значение несколько ниже - 0,7 обуславливая это необходимостью учета влияния дисперсии выборки (из-за возможных ошибок выборки). В нашем случае это правило "спасает" седьмую переменную - Средний возраст жителей.

Более интересный подход связан с построением Scree-графика по данным последней таблицы (пятой части TXT-отчета алгоритма PCA) PERCENT AND ACCUMULATIVE EIGENVALUES.


Рис. 6.8 Скриншот таблицы "Проценты и накопленные айгензначения" для 11 переменных

Таблица приводит абсолютные айгензначения и расчет процента общей дисперсии для каждого компонента (Рис. 6.8); в последнем столбце - накопленный процент объясненной дисперсии (суммарное значение - 100%). Очевидно, что в данном случае накопленное значение достигает 95% уже для трех главных компонент (Число хозяйств ниже уровня бедности, Индекс Джини, Число безработных афроамериканцев), на остальные 8 факторов приходится только 5% общей дисперсии.

Для более наглядного изображения можно построить график, где по горизонтали - номера главных компонент (начиная от 1-й), по вертикали - накопленный (ACCUMULATIVE) процент дисперсии, так называемый Scree Graf.



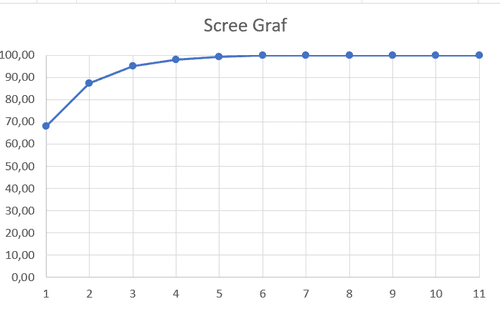
Рис. 6.9 Scree Graf, изображающий Накопленные айгензначения для 11 переменных

Название Scree Graf|График Осыпи происходит от сходства типичной формы с формой осыпи у подножия склона; критичной здесь является точка перелома графика отделяющая "склон" от субгоризонтального "плато" - в данном случае это точка пятой переменной (безработные афроамериканцы).

Подытоживая отметим: с одной стороны, большинство методов, предложенных для определения оптимального количества основных компонентов, подвергаются критике за эвристичность и субъективность, с другой - широко признается, что принятие окончательного решения остается за экспертом, выстраивающим геоинформационную модель. Так, Л. Феррье [Ferr´e, 1995], например, например, делает вывод, что не существует идеального решения, которое отвечало бы всем целям исследования, в то время как И.Т. Джоллифф [Jolliffe, 2002] вообще полагает, что основанные на статистике процедуры, по-видимому, не дают явных преимуществ по сравнению с суждениями опытных экспертов, хорошо знающих предметную область модели.


6.3. Исследовательская регрессия

Исследовательская Регрессия (ИР)|Exploratory Regression (ER) - это инструмент интеллектуального анализа данных, алгоритм, применяющий регрессию Метод Наименьших Квадратов (OLS) ко многим различным моделям, чтобы, выбрать те, которые проходят все необходимые диагностические тесты. Путем тестирования всех доступных моделей Исследовательская регрессия позволяет обнаружить независимые переменные, которые являются статистически значимыми в большинстве протестированных моделей. Для оценки результатов ИР и проверки нарушены ли допущения регрессии используются специальные тесты [Bajjali_2018].

Связь между зависимой переменной и предикторами (переменными-факторами), которую мы пытаемся установить с помощью линейной регрессии, гипотетически выглядит следующим образом:

Y: β0 + β1*X1 + β2*X2 + β3*X3 .... βi*Xi + ε
где:
Y - зависимая переменная (число убийство в квартале за 15 лет);
X - объясняющие|explanatory переменные (доход, индекс Джини, средний возраст и т.д.);
β - коэффициенты "бета", рассчитанные алгоритмом и выражающие силу и знак взаимосвязи между зависимой переменной и объясняющими переменными;
знак (+/-), связанный с коэффициентом (по одному для каждой объясняющей переменной), указывает, является ли связь положительной или отрицательной;
ε - остатки (residuals) или часть зависимой переменной, которая не объясняется моделью; модель ниже и выше прогнозов.

Исследовательская регрессия, если ее использовать разумно, позволяет оценить объясняющую способность каждой переменной, а также сравнивать сочетания переменных путем перекрестного сравнения моделей, и выбора тех, которые лучше отражают предположения о связи зависимой переменной с предикторами.

Приступим к моделированию. В общей сложности мы отобрали 11 независимых переменных, которые тестируются для моделирования зависимой переменной Преступность. Мы не определяем пока, какая из переменных будет окончательно включена в окончательную модель, вместо этого мы полагаемся на возможности анализа данных, которые предлагает исследовательская регрессия.

Алгоритм Exploratory Regression ArcMAP10.x отличается сложным интерфейсом и необходимостью заполнить несколько позиций диалогового окна: ArcToolbox >> Spatial Statistic Tools >> Modeling Spatial Relationships >> Exploratory Regression.

Exploratory Regression
Input Features: NYCTRACTs
Dependent Variable: Crime15y
Candidate Exploratory Variables: poorsqrt, giniIndex, ... *11 независимых переменных заключаются (Таблица 6.1)
Weights Matrix File: Leave empty. (*используется для вычисления пространственной автокорреляции остатков, если оставить это поле пустым, веса вычисляются на основе восьми ближайших соседей; эта весовая матрица не используется для расчета OLS)
Output Report File: ... Exploratory.txt
Output Results Table: Exploratory
Maximum Number of Explanatory Variable: 8 (*модель будет строиться максимум с четырьмя независимыми переменными)
Minimum Number of Explanatory Variable: 1
Minimum Acceptable Adj R Squared: 0.75
Maximum Coefficient p value Cutoff: 0.05
Maximum VIF Cutoff: 7.5
Minimum Acceptable Jargue Bera p value: 0.05
Minimum Acceptable Spatial Autocorrelation p value: 0.05
OK

Исследовательская регрессия выдает два файла - таблицу и отчет в TXT-формате: Main Menu >> Geoprocessing >> Results >> Current Session >> Exploratory Regression >> DC on Output Report File: Exploratory.txt. Отчет состоит из нескольких разделов.

Раздел 1: Краткое описание лучших моделей описывает три лучшие модели с самым высоким скорректированным R-квадратом и обеспечивает следующую диагностику (см. (Таблица 6.2).


Таблица 6.2 Диагностические тесты, используемые в исследовательской регрессии
Наименование диагностического теста Что обнаруживает Проверенная гипотеза (Когда значение p меньше уровня значимости, мы отвергаем нулевую гипотезу).
AICc corrected Akaike Information Criterion|Скорректированный информационный критерий Акайке Общая мера соответствия и как мера для сравнения различных моделей Модель, у которой наименьшее значение, обеспечивает наилучшую пригодность среди протестированных
P–значение JB (Jarque-Bera)|
Тест Жарка–Бера 		Нормальность остатков в качестве доказательства отсутствия смещенных остатков Нулевая гипотеза: нормальное распределение остатков(ошибок) регрессии
Альтернативная гипотеза: ненормальное распределение ошибок регрессии
BreuschPagan test|
Тест Бреуша–Пагана 		Проверка гетероскедастичности остаточных ошибок Нулевая гипотеза: постоянная дисперсия ошибки остатков (гомоскедастичность)
Альтернативная гипотеза: непостоянная дисперсия ошибки регрессии (гетероскедастичность)
Koenker’s studentized Breusch–Pagan K(BP)|
Статистика Кенкера (BP)		 P-значение, как мера гетероскедастичности Если ее значения меньше статистически значимых (p < 0,01), то смоделированные отношения не являются последовательными (либо из-за нестационарности, либо из-за гетероскедастичности)
Moran’s I|
Тест Морана I		 Определение, являются ли ошибки остатков пространственно автокоррелированными Нулевая гипотеза: нет пространственной автокорреляции в остаточных ошибках
Альтернативная гипотеза: существует пространственная автокорреляция в остаточных ошибках
VIF (variance inflation factor)|
Коэффициент инфляции дисперсии		 Для оценки мультиколлинеарности Указывается коэффициент инфляции с наибольшей дисперсией
SA -the p-value of the Global Moran’s I test|
P-значение глобального I-критерия Морана		 Для обнаружения пространственной автокорреляции Подтверждает либо опровергает нулевую гипотезу

Модели (если таковые имеются), прошедшие все тесты, помечены как Passing Models|Проходящие модели. Результаты сообщаются в соответствии с заданным значением "максимальное количество независимых переменных" (в данном случае мы указали 11) это означает, что Исследовательская регрессия проверит комбинации всех моделей, имеющих от одной независимой переменной до 11. Выходные данные включают три лучшие модели (вместе с пятью диагностиками) с одной независимой переменной, три лучшие модели с двумя независимыми переменными и так далее - до трех лучших моделей с одиннадцатью независимыми переменными. Кроме того, будут сообщены все проходящие модели. Если нет проходящих моделей, то последующие разделы раскрывают возможные причины, помогая определить, в каком направлении следует корректировать анализ.



Рис. 6.10 Фрагмент 1 раздела TXT-отчета исследовательской регрессии для 11 переменных

1-й раздел TXT-Report: интерпретация результатов. В этом разделе представлены три лучшие модели, которые имеют от одной до одиннадцати независимых переменных (мы установили это в качестве одного из наших параметров). Первая модель Choose 1 of 11 Summary связывает изучаемую зависимую переменную - Преступность - с единственной выбранной переменной-предиктором, которая указана в верхней строчке столбца Model - Доля домохозяйств ниже уровня бедности: только у этой переменной скорректированный R-квадрат >0,80. Вторая модель Choose 2 of 11 Summary - с двумя переменными, здесь проверку прошли три варианта сочетания двух факторов: (1) Доля домохозяйств ниже уровня бедности и Доля афроамериканского безработного населения, (2) Доля домохозяйств ниже уровня бедности и Среднегодовой доход домохозяйств, также (3) Доля лиц со степенью бакалавра и Доля домохозяйств ниже уровня бедности. Третья модель Choose 3 of 11 Summary предлагает три инварианта с тремя переменными (к уже перечисленным выше четырем факторам добавляются фактор Средний возраст жителей в разных сочетаниях).

Знаки перед переменными в столбце Model "+" означает положительную связь (+POORSQRT означает, что с ростом доли домохозяйств, живущих ниже уровня бедности, возрастает число убийств в квартале), знак "-" - отрицательную (-INCOME указывает, что с ростом среднегодового дохода домохозяйств в квартале число убийств снижается).

Таким образом, каждая последующая модель "богаче" предыдущей на привлеченные для объяснения зависимой переменной признаки: в модели Choose 4 of 11 Summary в трех инвариантах используется 6 признаков, хотя в каждом конкретном варианте используется число переменных заявленных в выборе, т.е., в данном случае - 4. Следует обратить внимание на то, как растет показатель AdjR2 - скорректированный коэффициент детерминации (процент вариации, объясняемый моделью, равен квадрату коэффициента корреляции) с добавлением новых переменных на каждом следующем шаге: Доля беднейших домохозяйств (1 из 11, т.е., как единственный фактор) выдает AdjR2 равный 0,82; при задействовании в модели четырех факторов AdjR2 равен 0,88, т.е., коэффициент детерминации вырастает на 0,04 и остается таковым (т.е., не оптимизируется - модель не объясняет больший процент выборки) на последующих шагах модели. Если скорректированный R-квадрат уменьшается, то привлеченные переменные скорее всего оказались бесполезны для модели.

Посмотрим на комбинаторику Choose 6 of 11 Summary


Рис. 6.11 Скриншот фрагмента 1 раздела TXT-отчета исследовательской регрессии - таблица для 6 переменных

Каждая из трех моделей (Рис. 6.11) для шести переменных немного отличается от двух других как набором факторов, так и их очередностью. Все три модели проходят (как и предыдущие - для меньшего числа переменных) имеют высокий Adjusted R-squared Results|Cкорректированный коэффициент детерминации AdjR2. Обратимся к другим индикаторам Отчета.

AICc corrected Akaike Information Criterion|Cкорректированный информационный критерий Акайке: легко заметить, что в вариантах моделей для любого количества переменных на первое место выведена модель с наименьшим критерием Акайке.

Следующий тест P–значение JB (Jarque-Bera)|P-значение Жарка-Бера или Критерий нормальности остатков, во всех наших тестах: 0,00 при установленном минимальном значении 0,05 и это значит, что модели не прошли проверку по этому критерию.

P-value Koenker’s studentized Breusch–Pagan K(BP)|P-значение Кенкера Брейша–Пагана - мера гетероскедастичности. Гетероскедастичность — понятие, означающее неоднородность наблюдений, выражающуюся в неодинаковой дисперсии случайной ошибки регрессионной модели. Когда статистика Кенкера (BP) статистически значима, существует гетероскедастичность и взаимосвязи модели ненадежны. В этом случае вместо P-значения t-статистики следует использовать t-статистику и Robust probabilities|Надежные вероятности, которые могут быть интерпретированы как P-значения, при этом значения меньше 0,01, являются статистически значимыми [Grekousis, 2020, p. 386].

VIF variance inflation factor|Коэффициент инфляции дисперсии используется для оценки мультиколлинеарности (потенциальной взаимосвязи объясняющих факторов-переменных); в вышеупомянутых моделях мультиколлинеарность не является проблемой, так как VIF во всех случаях меньше 4.

SA P-value of the Global Moran’s I test|P-значение глобального I-критерия Морана для обнаружения пространственной автокорреляции привлеченных переменных; в нашем случае 0,00.

2-й раздел TXT-Report - Exploratory Regression Global Summary|Общее резюме Исследовательской Регрессии. В этом разделе перечислены пять диагностик и процент моделей, прошедших каждый из этих тестов (Percentage of Search Criteria Passed). В случае, если ни одна модель не проходит, этот раздел помогает в выявлении потенциальных причин, по которым модели не работают должным образом. Например, если тест на нормальность не является статистически значимым для большинства моделей, то следует поставить под сомнение нормальность распределения как зависимой, так и независимых переменных. Кроме того, мы можем столкнуться с пространственно автокоррелированными остатками, которые указывают на отсутствующую (критически важную) переменную. Довольно часто эта пропущенная переменная является географической переменной, такой как расстояние от ориентира (например, расстояние от центра города), и тогда выход заключается в использовании Географически Взвешенной Регрессии.


Рис. 6.12 Скриншот Раздела 2 TXT-отчета исследовательской регрессии Exploratory Regression Global Summary

В рассматриваемых результатах регрессионного анализа обнаруживаются две серьезные проблемы: ни одна из 2035 моделей, построенных алгоритмом, не прошла тест на нормальность ошибок Jarque–Bera (минимальное значение 0,10), и тест на отсутствие пространственной автокорреляции (нулевая гипотеза Глобального индекса Морана).

3-й раздел TXT-Report: Summary of Variable Significance|Краткое описание значимости переменных. В этом разделе для каждая независимой объясняющей переменной (предиктора) указана ее значимость (определяемая коэффициентом детерминации) и характер связи с зависимой переменной:

1) % Significant|Процент (относительно числа всех протестированных) моделей, в которых переменная является статистически значимой (в соответствии с коэффициентом детерминации AdjR2);
2) % Negative|Процент моделей, в которых связь предиктора с зависимой переменной является отрицательной;
3) % Positive|Процент моделей, в которых связь предиктора с зависимой переменной является положительной.

Переменные с высоким процентом значимости являются сильными предикторами и, как правило, имеют один и тот же (положительный или отрицательный) знак связи с зависимой переменной. Переменные с небольшим процентом значимости, и зачастую "грешащие" непостоянством знака связи, перегружают модель и являются кандидатами на удаление.


Рис. 6.13 Скриншот Раздела 3 TXT-отчета Summary of Variable Significance исследовательской регрессии

В нашей модели две независимые переменные неизменно значимы и положительны в 100% моделей и могут считаться сильными предикторами феномена тяжких преступлений против личности: Доля хозяйств ниже уровня бедности, и Доля афроамериканского безработного населения. Сильные позиции и у пяти следующих переменных с устойчивым знаком связи:
Средний возраст населения MEDIANAGE (негативная связь - чем ниже возраст - тем больше совершается убийств);
Объемный след квартала FPRNTLOG (положительная связь - чем выше и плотнее здания в квартале - тем выше преступность);
Среднегодовой доход домохозяйств INCOME1000 (негативная связь - чем выше доход - тем ниже преступность);
Индекс Джини GINI_LG (положительная связь - чем выше значение индекса и более неравно распределены доходы - тем выше число убийств); Доля лиц с бакалаврской степенью BACHPRCNT (отрицательная связь).

Два последних признака - Общий уровень безработицы UNEMP_RATE и Число онкологических заболеваний CANCRSQRT не имеют постоянного знака и, как таковые, не являются надежными предикторами.

4-й раздел TXT-Report Summary of Multicollinearity|Краткое описание мультиколлинеарности сообщает, сколько раз две или более переменных с высокой мультиколлинеарностью включались в модель, обеспечивая тем самым одинаковый процент вариации. Оставляя только одну из таких переменных (как правило - с большим коэффициентом детерминации), мы избежим мультиколлинеарности и построим лучшую модель.


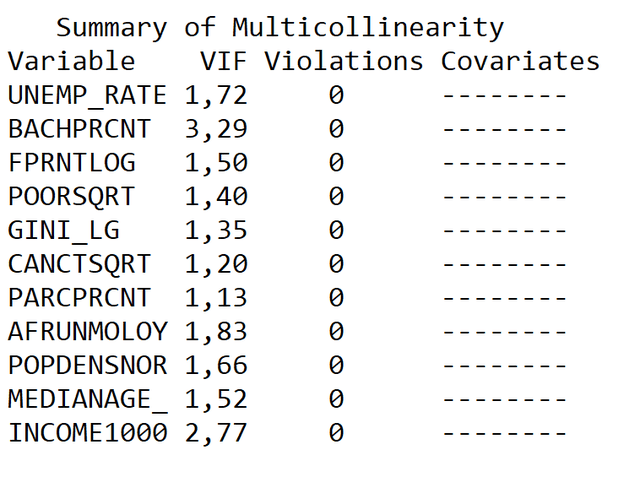
Рис. 6.14 Скриншот Раздела 4 TXT-отчета Summary of Multicollinearity Исследовательской регрессии

В нашей модели мультиколлинеарность не зафиксирована ни для одной из пар признаков - что свидетельствует о корректном выборе переменных по результатам проведенного ранее Анализа Главных Компонент.

5-й раздел TXT-Report представляет два теста: Summary of Residual Normality (JB)|Краткое описание диагностики Нормальности Ошибок и Summary of Residual Spatial Autocorrelation (SA)|Краткое описание Пространственной Автокорреляциии. В разделе приведены три модели, не обязательно прошедшие всю диагностику (passed models), но обладающие самыми высокими P–значениями Жака-Берра (нормальность ошибок) и три модели с самыми высокими P-значениями Морана I (пространственная автокорреляция). Этот раздел особенно полезен, если ни одна модель не проходит тесты. Проверяя P-значения теста Жарка–Берры и теста Морана I, мы оцениваем, насколько далека модель от выполнения предположений о наличии нормально распределенных остатков и нестационарных автокоррелированных остатков.

Вторым продуктом работы алгоритма Исследовательской регрессии является Exploratory Table (Results >> Exploratory Regression >> Output ResultTable), в которой суммируются все модели, преодолевающие пороговое значение Скорректированного коэффициента детерминации AdjR2, "отсекающее" значения VIF (Max VIF Value) и Cкорректированного информационного критерия Акайке (AICc). Каждая строка в таблице описывает модель, которая соответствует этим критериям, независимо от того, проходит ли она тесты в целом. Эта таблица полезна, в случаях, подобный рассматриваемому, когда мы рассматриваем возможность использования модели, хотя одно или несколько допущений не выполняются. Например, наиболее распространенным нарушенным предположением является нормальность ошибок. В таких случаях мы можем отсортировать таблицу по значениям AICc и использовать модель с минимальным значением критерия Акайке, которая при этом имеет лучшие показатели по другим диагностикам - прежде всего коэффициенту детерминации AdjR (Рис. 6.15).


Рис. 6.15 Скриншот экспортированной в Excel выводной таблицы Исследовательской Регрессии: значения отсортированы по минимальным значениям AICc и максимального скорректированного R-квадрат (коэффициент детерминации)

Лучшей моделью линейной регрессии для зависимой переменной с учетом всех изложенных обстоятельств, является модель с семью независимыми переменными, к числу которых относятся (в скобках указан знак связи):

  1. Доля домохозяйств ниже уровня бедности (+)
  2. Доля афроамериканского безработного населения (+)
  3. Средний возраст населения (-)
  4. Объемный след застройки (+)
  5. Среднегодовой доход домохозяйств (-)
  6. Индекс Джини (+)
  7. Доля лиц со степенью бакалавра (-)

Заключая раздел, посвященный возможностям простой линейной регрессии, мы должны вновь вспомнить на каких предположениях о характере связи между зависимой переменной и предикторами она основывается.

  • Связь между Y и X линейна при любом количестве привлеченных объясняющих факторов;
  • Предикторы независимы, т.е., между ними отсутствует автокорреляция, а остатки независимы друг от друга;
  • Распределение зависимой переменной и предикторов нормально;
  • Гомоскедастичность, т.е., дисперсия остатков не изменяется (увеличивается или уменьшается) с соответствующими значениями зависимой переменной.

В модели преступности Нью-Йорка под сомнение должны быть поставлены пункт 1, т.е., связь между преступностью и всеми привлеченными факторами, скорее всего не имеет простого линейного характера. Мы могли убедиться на парных точечных графиках, построенных в программе SAGA GIS, что при снижении Доходов домохозяйств Преступность действительно растет, но только до определенного предела, после которого достигается небольшое плато, а при дальнейшем росте бедности - падает; иными словами, очень бедные люди в той же мере не склонны к совершению тяжких преступлений, как и весьма обеспеченные. К сожалению, наши данные не соответствуют в должной степени и пункту 3 (нормальность распределения). В итоге полученная нами модель хоть и представляет интерес с точки зрения исследования самого феномена, но не может считаться ни законченной, ни исчерпывающей.


6.4. OLS - Метод наименьших квадратов

Ordinary Least Squares (OLS)|Метод наименьших квадратов (МНК) - это статистический метод оценки неизвестных параметров (коэффициентов) модели в уже рассмотренном нами уравнении линейной регрессии. Регрессия OLS определяет эти значения путем минимизации суммы квадратов вертикальных расстояний от наблюдаемых точек до прямой линии регрессии (сумма квадратов остатков) и также называется Линейной регрессией OLS или просто Линейной регрессией.

Запустим OLS для семи переменных, преодолевших барьер Summary of Variable Significance 90%, выбранных с помощью Исследовательского регрессионного анализа:

  1. Доля домохозяйств ниже уровня бедности,
  2. Доля афроамериканского безработного населения,
  3. Средний возраст населения,
  4. Объемный след застройки,
  5. Среднегодовой доход домохозяйств,
  6. Индекс Джини,
  7. Доля лиц со степенью бакалавра.
ArcToolbox >> Spatial Statistic Tools >> Modeling Spatial Relationships >> Ordinary Least Squares
Ordinary Least Squares
Input Feature Class: NYCTRACTs (*файл кварталов Нью-Йорка с необходимыми полями зависимой переменной и предикторов)
Unique ID Field: ID
Output Feature Class: ... OLS_7values.shp
Dependent Variable: Murdr15y (*изучаемая зависимая переенная)
Explanatory Variable: poorsqrt, afrunmploysrt, medianage ....income (*набор объясняющих независимых переменных-предикторов
Output Report File: ... OLS7values.pdf
Additional Options:
Coefficient Output Table: ... OLS7valCoefficient
Diagnostic Output Table: ... OLS7valDiagnostics
Output Report File: OLS7values.pdf
OK

Отчет алгоритма доступен как обычно во вкладке результаты: Main Menu >> Geoprocessing >> Results >> Current Session >> Ordinary Least Squares >> RC on Output Report File: OLS7values.pdf.

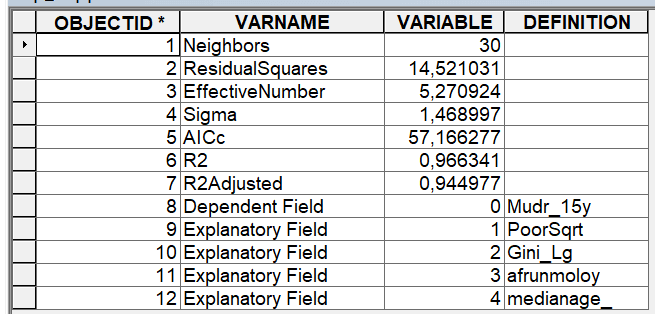
1-й раздел отчета Summary of OLS Results - Model Variables - представляет таблицу значений индексов, которые уже знакомы нам по алгоритму Explanatory Regression для использованных переменных (предикторов) модели.


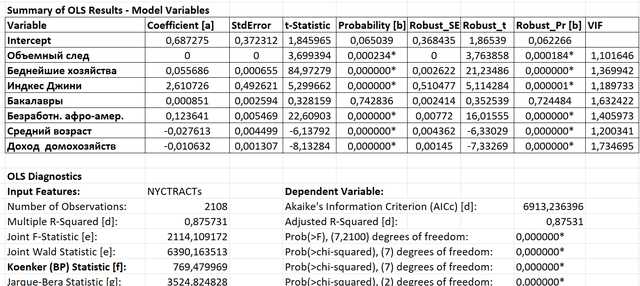
Рис. 6.16 Скриншот Раздела 1 Summary of OLS Results - Model Variables и 2 Summary of OLS Diagnostics PDF-отчета Метода наименьших Квадратов (таблица экспортирована в Excel)

Интерпретация первого раздела тесно связана со вторым разделом (что объясняет сплошную индексацию буквами английского алфавита: [a] в Summary of OLS Results - Model Variables и [d] во второй части раздела OLS Diagnostics. При интерпретации необходимо учитывать следующие позиции, изложенные в PDF-отчете инструмента под таблицей OLS-Диагностики (Notes on Interpretation) [Grekousis, 2020]:

[a] Коэффициенты (это и есть те самые β-бета множители перед переменными в формуле линейной регрессии): представляют силу и тип взаимосвязи между каждой объясняющей переменной и зависимой переменной. Звездочка рядом с цифрой указывает на статистически значимое значение P (P < 0,01).
[b] Вероятность и надежная вероятность (robust_Pr): звездочка (*) указывает, что коэффициент статистически значим (P < 0,01); если статистика Кенкера (BP) [f] статистически значима, используем столбец Надежной вероятности (robust_Pr) для определения значимости коэффициента.
[c] Коэффициент инфляции дисперсии (VIF): значения Коэффициента инфляции большой дисперсии (VIF) (> 7,5) указывают на избыточность среди объясняющих переменных.
[d] Коэффициент детерминации R-Квадрат, Скорректированный Коэффициент детерминации AdjR2 и Информационный критерий Акайке (AICC): показатели производительности и соответствия модели.
[e] Совместная статистика F и Вальда: звездочка (*) указывает на общую значимость модели (P < 0,01); если статистика Кенкера (BP) [f] статистически значима, используйте статистику Вальда для определения общей значимости модели.
[f] Статистика Кенкера (BP): когда этот тест статистически значим (P< 0,01), моделируемые взаимосвязи не являются согласованными (либо из-за нестационарности, либо гетероскедастичности). Следует полагаться на надежные вероятности (robust_Pr) для определения значимости коэффициента и на статистику Вальда для определения общей значимости модели. Когда тест Кенкера статистически значим, это означает, что одна или несколько объясняющих переменных распространены закономерно в географическом пространстве и, следовательно, модель может быть улучшена с использованием географически взвешенной регрессии.
[g] Статистика Жарка-Бера: когда этот тест статистически значим (P < 0,01), предсказания модели смещены (остатки распределены ненормально).

Краткие указания, изложенные в этом списке обычно составляют содержание интерпретации результатов регрессионной модели в руководствах по ArcMAP10.x [Bajjali, 2018; Pimpler, 2017]. Вообще говоря, уже первая колонка таблицы Summary of OLS Results - Model Variables (первый раздел PDF-отчета) представляет нам искомые бета-коэффициенты для переменных уравнения регрессии (Y по X), однако, прежде чем их использовать необходимо разобраться в результатах детально и заглянуть чуть глубже в результаты отчета.

Number of Observations|Число Наблюдений в OLS Diagnostics как легко догадаться означают просто общее количество объектов в модели - в данном случае общее число кварталов Нью-Йорка, обеспеченных значениями соответствующих переменных.

Multiple R-Squared [d]|Множественный R-квадрат является уже знакомым нам коэффициентом детерминации - мера объясненной вариации или величины вариации переменной Y, которую можно смоделировать с помощью линейной зависимости от X.

Сумма квадратов регрессии, также называемая Объясненной вариацией (модели) рассчитывается как:

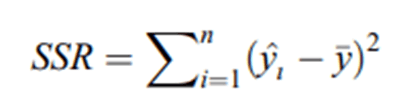
Это мера Объясненной вариации или величины вариации Y, которую можно смоделировать с помощью линейной зависимости от X.

Сумма квадратов ошибок, также называемая Необъяснимой вариацией или остаточной суммой квадратов:

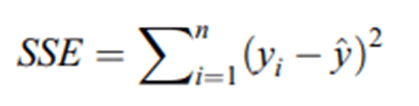
Тогда Общая вариация Y может быть рассчитана как:


Общая вариация = Объясненная вариация регрессией + Необъясненная вариация, или:
SST: SSR + SSE

Коэффициент детерминации, обозначаемый как R2 (R-квадрат), представляет собой процент вариации, объясняемой моделью. Он рассчитывается как отношение между изменением прогнозируемых значений зависимой переменной (Объясненная вариация SSR) к изменению наблюдаемых значений зависимой переменной. Он равен квадрату коэффициента корреляции.

R2= SSR/SST

Проще говоря, это частное от деления квадрата суммы разницы прогнозируемых значений Yi со средним значением наблюдаемых Y (квадрат суммы регрессии), на квадрат суммы разницы наблюдаемых значений Yi со средним значением наблюдаемых Y.

Коэффициент детерминации рассчитывается по формуле:

R 2= 1 - (SSE/SST)

Поскольку остаточная сумма квадратов минимизируется в обычной регрессии наименьших квадратов, отношение SSE/SST всегда меньше 1. Чем меньше Необъясненная вариация SSE, тем меньше соотношение в уравнении и тем больше Коэффициент детерминации, и, следовательно, Объясненная вариация. Чем больше значение коэффициента, тем надежнее модель. Нулевое значение указывает на то, что изменение зависимой переменной не объясняется и, скорее всего, модель не может быть использована, в то время как значение 1 объясняет всю изменчивость данных, идеально вписывающуюся в линию на точках данных. Например, если R-квадрат равен 82%, это обычно означает, что 82% вариации Y обусловлено изменениями значений X, что означает, что X является хорошим предиктором для Y, имеющим вероятностную линейную зависимость [Pimpler, 2017].

Так как модель линейной регрессии соответствует линии для минимизации так называемых Остатков (Residuals), идеальное соответствие приведет к нулевым остаткам. Когда остатки невелики, у нас есть хорошая подгонка линии. По мере увеличения остатков модель становится менее надежной; она выдает прогнозируемые значения, которые сильно отклоняются от наблюдаемых.

В общем случае, когда переменные не коррелируют, ожидается, что каждая из них будет объяснять различную величину вариации зависимой переменной. Тем не менее, переменные редко бывают некоррелированными: условно - в рамках конкретной модели - привлеченные к объяснению переменные считаются "независимыми", но по большому счету мы никогда не знаем этого наверняка. Г. Грекоузис [Grekousis, 2020] предлагает наглядное графическое объяснение Коэффициента Детерминации R-квадрат.


Рис. 6.17 Графическая репрезентация феномена изменчивости зависимой переменной от нескольких предикторов, источник [Grekousis, 2020]

Рисунок (Рис. 6.17) хорошо объясняет различную роль нескольких предикторов в объяснении зависимой переменной Y. В случаях (A) простой линейной регрессии переменная X1 объясняет часть a вариации независимой переменной Y с помощью простой линейной регрессии. В множественной линейной регрессии (B) включение второй переменной X2 приводит к дополнительному объяснению b части вариации, причем той, которую не объясняла переменная X1. Общая объясненная вариация R2 равна a + b. В ситуации (C) при том же числе предикторов (2) существует перекрывающаяся часть c вариации Y, которая объясняется обеими независимыми переменными, поэтому ее следует включать только один раз в общую объясненную вариацию. Иными словами в модель должна быть включена только неперекрывающаяся часть вариации, объясненной через X2, а именно "b - c", и тогда общий объем объясненной R2 равен a +(b - c). В ситуации (D) X1 и X2 сильно коррелируют и объясняют почти одинаковую долю вариации, дополнительная вариация, объясненная при включении X2 в модель, является частью d. Конечный объем объясненной вариацииR2 равен "a + d", где a - изменение, объясняемое X1, а d - не перекрывающееся изменение между X1 и X2. Если X1 объясняет 80% вариации, то при добавлении X2 объясненная вариация увеличивается до 82%. Обычно это означает, что X2 помогает объяснить дополнительные 2% объясненной вариации, а не то, что X2 объяснил бы 2%, если бы X1 если бы был включен в качестве единственного фактора в другую модель.

Небольшой Коэффициент Детерминации не обязательно является признаком недостаточной регрессионной модели. То, как мы интерпретируем R-квадрат, зависит от масштабов исследования и исследовательских вопросов. Следует иметь ввиду, что для определения взаимосвязей между зависимыми и независимыми переменными может быть полезен даже низкий R-квадрат, поскольку и такая, модель все еще может иметь статистически значимые независимые переменные (низкие P-значения). Другими словами, при низком процентном значении Объясненной вариации взаимосвязи могут все еще существовать, и как таковая модель будет полезна для выявления тенденций. По этой причине R2всегда следует оценивать с использованием графика остатков [Grekousis, Gialis, 2018].

В нашей модели R2 равен 0,876, что казалось бы означает что модель объясняет почти 88% вариации зависимой переменной. Однако R-квадрат не дает представления о том, насколько статистически значима гипотетическая взаимосвязь. Для этого используется F-критерий общей значимости

Еще одна близкая по функции оценка Adjusted R-Squared|Скорректированный R-Квадрат — это Коэффициент детерминации, скорректированный на количество переменных, так как каждая добавленная переменная увеличивает объясненную вариацию зависимой переменной. Как R-квадрат, так и Скорректированный R-квадрат, используются для оценки процента общего объясненного отклонения. Тем не менее, между ними есть существенная разница. В то время как R-квадрат предполагает, что каждая отдельная переменная объясняет изменение Y, скорректированный R-квадрат объясняет процент вариации только тех независимых переменных, которые влияют на Y. R-квадрат имеет тенденцию увеличиваться с каждой дополнительной переменной, что приводит нас к неправильному выводу о том, что мы создаем лучшую модель. Фактически, добавляя все больше и больше переменных, мы сталкиваемся с проблемой избыточности данных и перегрузки модели. Использование Скорректированного AdjR2, позволяет определить, какие переменные полезны, а какие нет, и рассмотреть возможность сохранения только тех переменных, которые увеличивают именно Скорректированный R-квадрат. Для сравнения исследователь всегда может добавить новую переменную и запустить OLS с расширенным набором переменных: например, в данной модели добавление переменной Общий уровень безработицы увеличивает R2 только на 0,012. Тем не менее, согласно Adjusted R-Squared [d]: наш набор из семи переменных объясняет 87,5% тяжких преступлений в Нью-Йорке.

В отчете OLS приводится также величина Standard Error (Deviation) of Regression|Стандартная ошибка оценки, представляющая собой квадратный корень из суммы квадратов ошибок, разделенной на степени свободы:


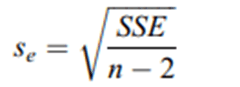
Показатель Стандартная ошибка демонстрирует насколько близко или далеко в среднем находятся наблюдения от линии наименьших квадратов. Примерно 95% наблюдений должны находиться в пределах двух стандартных ошибок от линии регрессии. В этом отношении мы можем использовать стандартное отклонение регрессии в качестве приблизительной оценки 95% интервала прогнозирования. Стандартная ошибка регрессии имеет те же единицы измерения, что и зависимая переменная. Предпочтительны более низкие значения стандартных ошибок, указывающие на меньшие расстояния между точками данных и подобранными значениями. Комбинируя R-квадрат и Стандартную ошибку регрессии, мы можем лучше оценить достоверность нашей модели. В некоторых случаях невысокое значение R2может компенсироваться низкими значениями StdError. Так в нашей модели значение Стандартной ошибки оказались большим только для одной переменной Индекса Неравенства Доходов Джини (0,492621 при минимальном значении 0,0 и максимальном - 1.

F-Test of the Overall Significance|F-Критерий общей значимости. Статистика F-критерия общей значимости модели, оценивает, являются ли коэффициенты регрессии Метода Наименьших Квадратов статистически значимыми.


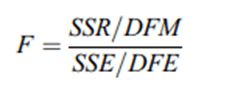
где SSR — это мера объясненной вариации из квадратичной регрессии,
SSE - необъясненная вариации или сумма квадратов ошибок,
DFM: p - 1 степень свободы для модели, где p - количество параметров модели,
DFE: n - p это степени свободы для ошибки, где n - количество наблюдений.

В контексте регрессионного анализа большие или низкие значения F-статистики не указывают на какую-либо значимость модели; содержательные выводы могут быть сделаны только при сравнении конкретных значений с пороговыми P-значениями. Если F-статистика мала (например, менее 0,05), то мы можем отвергнуть нулевую гипотезу и принять, что регрессионная модель статистически значима. В этом случае мы утверждаем, что наблюдаемая тенденция не обусловлена случайной выборкой из множества наблюдений. Если значение F-статистики велико (например, больше 0,05), то мы не можем отвергнуть нулевую гипотезу. В этом случае мы должны быть осторожны в том, как интерпретировать результаты, поскольку невозможно определенно утверждать, что между Y и X отсутствует зависимость. В этом случае остаются вероятными три гипотезы [Grekousis, Gialis, 2018]:

  1. Между X и Y нет линейной зависимости. Тем не менее, может существовать нелинейная зависимость, например, экспоненциальная или логарифмическая.
  2. Переменная X может объяснить небольшую часть вариации Y, но этого недостаточно, чтобы считать модель статистически значимой, используя только X. Возможно, нам потребуется добавить еще несколько переменных, чтобы объяснить Y.
  3. Линейная зависимость все же существует, но размер нашей выборки слишком мал, чтобы ее можно было обнаружить

В нашей модели F-критерий общей значимости характеризуется в разделе OLS Diagnostics (Рис. 6. 16) тремя показателями: Joint F-Statistic 2114,109 (само по себе ни о чем не говорящее значение); Prob (>F) 7,2100 degrees of freedom (число степеней свободы); Статистическая значимость 0,000000 т.е., менее 0,05. Таким образом, мы можем отвергнуть нулевую гипотезу и принять, что регрессионная модель статистически значима

t-Statistic (Coefficients’ Test)|t-статистика или Тест Коэффициентов. t-статистика в регрессионном анализе — это статистика, используемая для проверки того, является ли коэффициент b уравнения линейной регрессии статистически значимым - для решения вопроса о том, какие независимые переменные оставить в модели, а какие - исключить..

t = b / SEb
где SEb - стандартная ошибка расчетного коэффициента b

Однако, прежде чем мы оценивать t-статистику, необходимо проверить статистику Кенкера (BP) [Koenker, Hallock, 2001]. Если статистика Кенкера (BP) статистически значима, то делается вывод о существовании гетероскедастичности, и взаимосвязи модели признаются ненадежными. В этом случае вместо P-значения t-статистики следует использовать Robust t-statistic|Робастную статистику и Robust probabilities|Надежные вероятности (рассчитываемые автоматически). Робастные (заслуживающие доверия, надежные) вероятности могут быть интерпретированы как P-значения, при этом значения, например, меньше 0,01 являются статистически значимыми.

Для небольшого P-значения t-статистики мы отвергаем нулевую гипотезу о том, что коэффициент b равен нулю, и принимаем его значение как статистически значимое. В этом случае независимая переменная X, которой присваивается коэффициент, важна для расчета зависимого Y. Для большого P-значения мы не можем принять b как статистически значимое, и нам следует рассмотреть возможность удаления соответствующей независимой переменной из модели.

Во втором разделе PDF-отчета OLS Diagnostics (Рис. 6. 16) предпоследнюю строчку занимает Статистика Кенкера. В нашей модели Koenker (BP) Statistic [f] равна 769,479969 при Prob(>chi-squared) 0,000000* и семи степенях свободы (т.е., статистическая значимость менее 0,01).

Следовательно, моделируемые взаимосвязи не являются согласованными (либо из-за нестационарности, либо гетероскедастичности). Мы должны полагаться на надежные вероятности (robust_pr) для определения значимости коэффициента и на статистику Вальда для определения общей значимости модели.

Wald Test (Coefficients’ Test)|Тест Вальда (Тест коэффициентов). Если тест отклоняет нулевую гипотезу (значение P меньше уровня значимости), то мы принимаем, что коэффициент b не равен нулю, и, таким образом, мы можем включить соответствующую переменную в модель. Если нулевая гипотеза не отвергнута, то удаление соответствующей переменной существенно не повредит эффективности модели.

Тест Вальда может быть дополнительно применен для проверки совместной значимости нескольких коэффициентов, и именно поэтому он также называется совместным (joined) тестом Вальда. Тест Вальда следует проверять вместо F-значимости, когда статистика Кенкера (АД) статистически значима. Если значение P невелико, это свидетельствует о высокой общей производительности модели.

В нашей модели (Рис. 6. 16) Joint Wald Statistic [e] равен 6390,163513 при Prob(>chi-squared 0,000000*, т.е., модель обладает достаточно высокой производительностью и мы принимаем общую значимость модели с высоким Коэффициентом Детерминации Adjusted R2 [d] равным согласно OLS Diagnostics 0,87531.

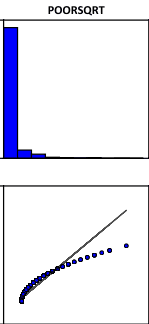
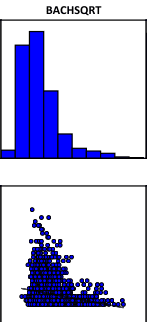
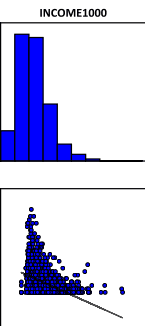
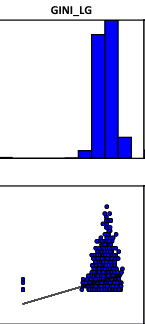
Следующий третий раздел PDF-отчета Variable Distributions and Relationships|Распределение и Взаимосвязи Переменных включает Диаграммы Рассеяния. Каждая диаграмма рассеяния отображает взаимосвязь между объясняющей переменной и зависимой переменной. Сильные связи отображаются в виде диагоналей, а направление наклона указывает, является ли связь положительной или отрицательной. По замыслу ESRI [Bajjali, 2018] диаграммы позволяют обнаружить какие-либо нелинейные взаимосвязи, хотя, разумеется это можно (и нужно) делать на стадии Исследовательского Анализа Данных. Графики раздела представляют собой гистограммы и диаграммы рассеяния для каждой пары объясняющей и зависимой переменных (Рис. 6.18). Гистограммы показывают, как распределена каждая переменная. OLS не требует, чтобы переменные были нормально распределены, если возникают проблемы с поиском правильно заданной модели, можно попробовать преобразовать сильно искаженные переменные, чтобы увидеть, получите ли вы лучший результат.



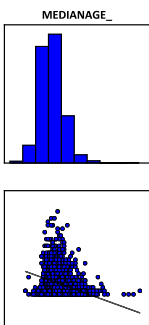
Рис. 6.18 Гистограммы и Диаграммы Рассеяния для каждой объясняющей переменной и зависимой переменной в PDF отчете, слева направо верхний ряд - Доля домохозяйств ниже уровня бедности, Доля лиц со степенью бакалавра, Объемный след; нижний ряд - Среднегодовой доход домохозяйств, Индекс неравенства доходов Джини, Средний возраст жителей

Далее в PDF-отчете приведена Histogram of Standardized Residuals|Гистограмма стандартизированных Остатков, сопровождающаяся следующей справкой "В идеале гистограмма ваших остатков должна соответствовать нормальной кривой, указанной выше синим цветом. Если гистограмма сильно отличается от нормальной кривой, возможно, у вас предвзятая модель. Если это смещение является значительным, оно также будет представлено статистически значимым P-значением Jarque-Bera(*)".



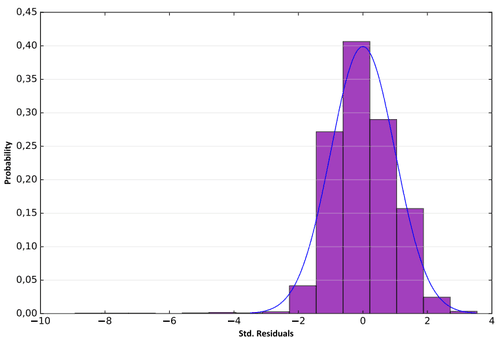
Рис. 6.19 Гистограмма стандартизированных остатков

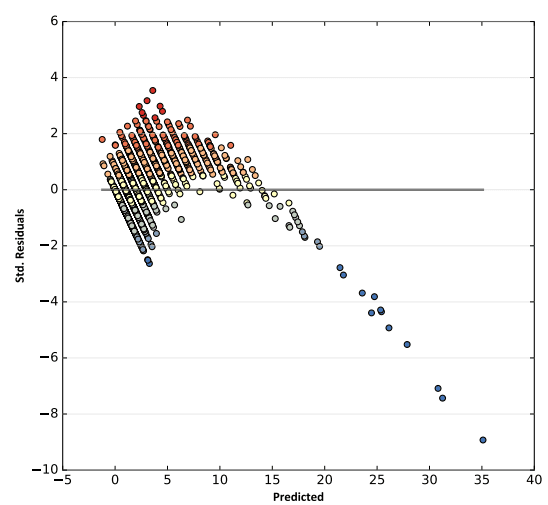
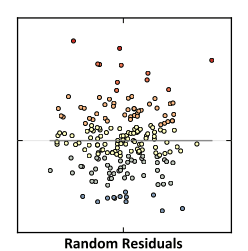
Заключительный раздел PDF-отчета Метода Наименьших Квадратов содержит два графика. График Received Residual vs. Predicted Residual (Полученных Остатков против Ожидаемых Остатков): значения выше и ниже прогнозируемых по отношению к значениям зависимых переменных.



Рис. 6.20 График Полученных Остатков против Ожидаемых и график Рандомных Остатков (для сравнения)

График сопровождается "подсказкой": "Для правильно заданной модели эта диаграмма рассеяния будет иметь небольшую структуру и выглядеть случайной. Если в этом сюжете есть структура, тип структуры может быть ценным ключом, который поможет вам понять, что происходит". В нашей модели (Рис. 6.20) явно прослеживается искажение, свидетельствующее о нелинейном характере связи между зависимой переменной и предикторами.


`
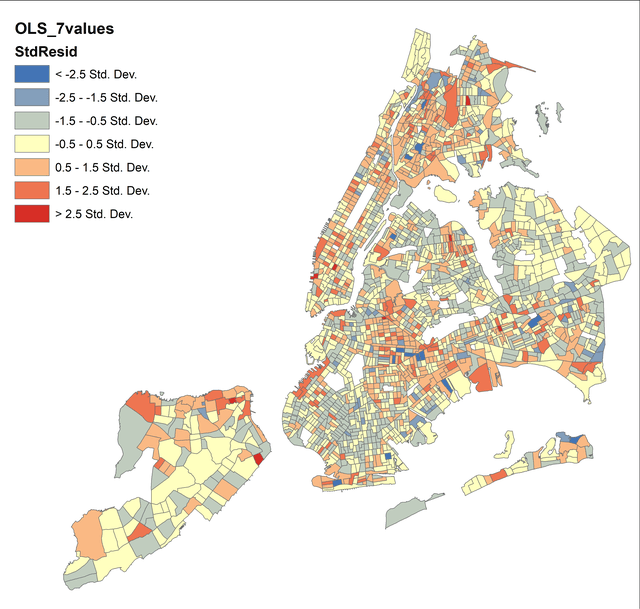
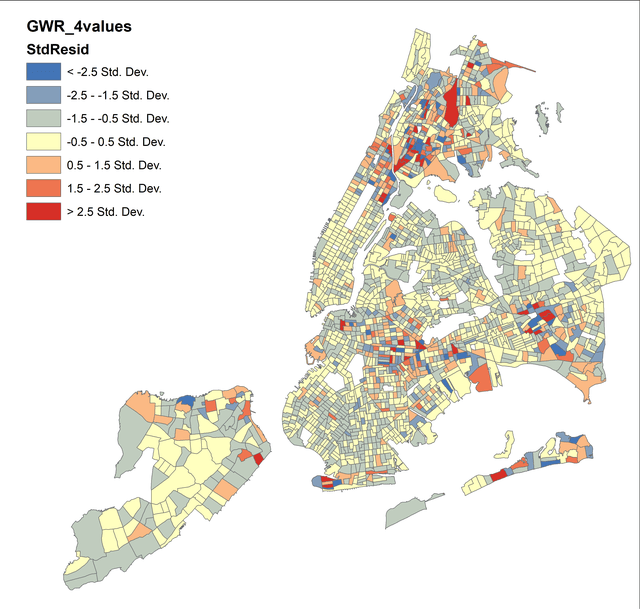
Рис. 6.21 Картограмма стандартизированных остатков

Мы можем верифицировать наши выводы и по Картограмме Стандартизированных Остатков, являющейся вторым (кроме PDF-отчета) результатом работы инструмента OLS regression. Особое внимание следует обратить на распределение кварталов, характеризующихся более чем 2,5 стандартными отклонениями в большую или меньшую сторону (такие полигоны закрашиваются в ярко-красный и синий цвета соответственно)

В качестве дополнительной процедуры мы можем подвергнуть векторный слой Стандартизированных Остатков проверке инструментом Пространственная автокорреляция Морана I с предварительным созданием файла пространственных весов.

ArcToolBox >> Spatial Statistics Tools >> Modeling Spatial Relationships >> Generate Spatial Weights Matrix
Input Feature Class: ... OLS7values
Unique ID Field: ID
Output Spatial Weights Matrix File: ... SW_OLS7.swm
Conceptualization of Spatial Relationships: K_NEAREST_NEIGHBORS
Distance Method: EUCLIDEAN
Number of Neighbors: 8
Row Standardization: Check
OK

Далее рассчитываем Пространственную Автокорреляцию Морана|Spatial Autocorrelation (Morans I):

ArcToolbox >> Spatial Statistic Tools >> Analyzing Patterns >Spatial Autocorrelation (Morans I)
Input Feature Class: OLS7values
Input Field: Residual
Generate Report: Check
Conceptualization of Spatial Relationships: GET_SPATIAL_WEIGHTS_FROM_FILE
Weights Matrix File: ... SW_OLS7.swm
OK
Результаты Пространственной Автокорреляции Морана:
Moran's Index: 0,100643
Expected Index: -0,000475
Variance: 0,000109
z-score: 9,677551
p-value: 0,000000


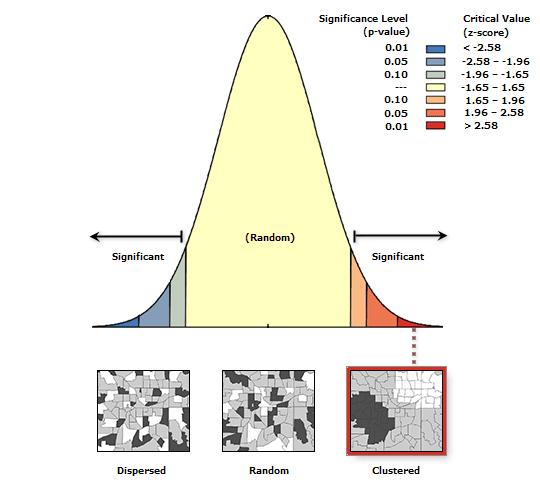
Рис. 6.22 График распределение P-значения и Z-оценки для Пространственной Автокорреляции остатков

"Подсказка" свидетельствует: Учитывая z-балл 9,67755093533, вероятность того, что этот кластеризованный шаблон может быть результатом случайной случайности, составляет менее 1%. Иными словами, наши остатки имеют выраженное кластерное распределение

Подведем итоги в виде таблицы - своего рода алгоритма для сверки полученных результатов. Формально мы можем считать результатом регрессионного анализа используя следующую формулу регрессии - она следует из значений коэффициентов - столбец (a) Summary of OLS Results - Model Variables:

Y = 0,687 + 0 FOOTPRNT + 0,056 POOR + 2,61 GINI + 0,0008 BACHEL + 0,124 AFROAMUNEPL - 0,028 MEDIANAGE - 0,01 INCOME

Очевидно, что из этой модели без ущерба для результата можно исключить Объемный след застройки FOOTPRNT и Долю лиц со степенью бакалавра BACHEL

Таблица 6.3 Матрица для сверки результатов регрессионного анализа
Индикаторы Значение Значимость Интерпретация Примечание
R-Squared:
Общая состоятельность
модели		 0,8757 (+) ---- Модель объясняет 87,6 % вариации зависимой переменной Murdr5y Следует проверить Скорректированный R-квадрат
Adjusted
R-Squared:
Общая состоятельность
модели		 0,8753 (+) ---- Скорректированный R-квадрат равен 0,8753, что указывает на высокую степень подгонки, еще одно подтверждение, что Модель объясняет 87,5 %вариации зависимой переменной Необходимость добавления дополнительных переменных для лучшей подгонки модели отсутствует
Joint F-Statistic
: Совместная
F-статистика 		2114,1 (+) 0,000000* (тест значим на уровне 0,01) Нулевая гипотеза отвергается, регрессионная модель статистически значима: тенденция является реальным эффектом, а не результатом случайной выборки данных Необходима дополнительная перепроверка с помощью совместной статистики Вальда, особенно если тест Кенкера (КБ) является статистически значимым
Joint Wald Statistic
Совместная
Статистика Вальда		 6390,2 (+) 0,000000* (тест значим уровне 0,01) Совместный тест Вальда статистически значим и подтверждает общую валидность модели статистика Вальда использована для анализа общей производительности модели, поскольку Koenker (BP) Statistic [f] статистически значима (р <0,05)
Akaike's Information
Criterion (AICc)
Акайке Исправленный критерий(AICC)		 6913,2 (+) ---- AICc — это показатель качества моделей для одного и того же набора данных, AICcуказывает на лучшее соответствие, когда значения уменьшаются. Может быть использован для изменения набора переменных, сравнения различных моделей и выбора наиболее подходящей
Coefficient [a]
бета-коэффициенты
- множители переменных		 Probability [b]:
FOOTPRNT 0 0,000234*
POORSQRT 0,055686 0,000000*
GINI_LG 2,610726 0,000000*
BACHSQRT 0,000851 0,742836
AFRUNMPLOY 0,123641 0,000000*
MEDIANAGE -0,027613 0,000000*
INCOME -0,010632 0,000000*
Значима на уровне, не превышающем 0,01 Все переменные значимы, за исключением BACHSQRT, знаки коэффициентов совпадают с ожиданиями Поскольку статистика Koenker (BP) статистически значима, в оценке достоверности значений бета-коэффициентов необходимо использовать надежные вероятности \ robust probabilities (Probability [b]); переменную Доля лиц со степенью бакалавра можно исключить из модели
Coefficients
t-statistic
Коэффициенты
t-статистика		 Probability [b]: FOOTPRNT 0,000234* POORSQRT 0,000000* GINI_LG 0,000000* BACHSQRT 0,742836 AFRUNMPLOY 0,000000* MEDIANAGE 0,000000* INCOME 0,000000* Значима на уровне не превышающем 0,01 Все переменные значимы, за исключением BACHSQRT Поскольку статистика Koenker (BP) статистически значима, вместо этого привлечены надежные вероятности \ robust probabilities (Probability [b]); переменную Доля лиц со степенью бакалавра можно исключить из модели
Standard Errors
(Robust probabilites) Cтандартные Ошибки (надежные вероятности)		 Robust_Pr [b]: FOOTPRNT 00,000184* POORSQRT 0,000000* GINI_LG 0,000001* BACHSQRT 0,724484 AFRUNMPLOY 0,000000* MEDIANAGE 0,000000* INCOME 0,000000* Значима на уровне не превышающем 0,01 Все переменные значимы, за исключением BACHSQRT Шесть переменных с коэффициентами Std. Err. (Robust probabilites), прошедшими тест могут считаться устойчивыми к гетероскедастичности
Variance Inflator
Factor|Мультиколлинеарность		 VIF: FOOTPRNT 1,101646 POORSQRT 1,369942 GINI_LG 1,189733 BACHSQRT 1,632422 AFRUNMPLOY 1,405973 MEDIANAGE 1,200341 INCOME 1,734695 VIF: 1-4 коллинеарность отсутствует
VIF: 4-10 требуется дополнительный анализ
VIF > 10 наблюдается значительная коллинеарность
 Все переменные имеют значения меньше, чем 4; отсутствие проблем с мультиколлинеарностью К модели не следует добавлять дополнительные переменные, из уже привлеченных чуть более высокое значение имеют INCOME и BACHSQRT - возможные кандидаты на удаление
Normality of residual
errors Jarque–Bera|
Статистика Жарка-Бера Нормальность остаточных ошибок 		3524,8 Prob(>chi-squared), (2) degrees of freedom: 0,000000* Значим на уровне 0,01
 Нулевая гипотеза (нормальность ошибок) должна быть отвергнута, поскольку значение теста статистически значимо. Предвзятая модель с нарушенные условием о нормальности ошибок, возможно также что в модели не хватает одной или нескольких ключевых переменных
Heteroscedasticity
Koenker–Bassett test
|Гетероскедастичность тест Кенкера		 0,000000* Значим на уровне 0,01
 Нулевая гипотеза (гомоскедастичность) должна быть отвергнута, поскольку значение теста статистически значимо Взаимоотношения зависимой переменной через предложенные коэффициенты (Coefficient [a]) не являются согласованными; отношения между некоторыми или всеми объясняющими переменными и зависимой переменной нестационарны)
Spatial Dependence
Moran’s I		 0,100643 Значим на уровне 0,01
 Не значимы Отсутствуют достаточные основания для опровержения гипотезы об отсутствии пространственной автокорреляции

Таким образом, по результатам анализа мы можем как минимум - скорректировать нашу модель:

Y: 0,687 + 0,056 POOR + 2,61 GINI + 0,124 AFROAMUNEPL - 0,028 MEDIANAGE - 0,01 INCOME

Модель не прошла тестирование по двум важными параметрам тесту Кренкера и тесту Жарка-Барра. Когда тест Кенкера статистически значим, как здесь, это указывает, что отношения между некоторыми или всеми объясняющими переменными и зависимой переменной нестационарны. Например, переменная Индекс Джини может быть важным предиктором количества тяжких преступлений в некоторых кварталах Нью-Йорка, но, возможно, слабым предиктором в других местах. В этих случаях рекомендуется улучшить результат модели, перейдя к географически взвешенной регрессии.


6.5. Географически взвешенная регрессия

Необходимость (и возможность) использования Географически Взвешенной Регрессии GWR для данного набора данных объясняется значимостью тест Кенкера или гетероскедастичностью. В процедуре GWR можно использовать оптимизированный набор переменных удалив из него - согласно результатам OLS - показатель не прошедший два важных теста - Долю лиц со степенью бакалавра. В итоге для объяснения зависимой переменной - числа тяжких преступлений в кварталах Нью-Йорка у нас остается шесть факторов. Интерфейс инструмента GWR несколько отличается от двух предыдущих видов регрессии

ArcToolbox >> Spatial Statistic Tools >> Modeling Spatial Relationships >> Geographically Weighted Regression
Input Feature Class: NYCTRACTs
Dependent Variable: Murdr15y
Explanatory Variable: poorsqrt, ... medianage (*6 переменных)
Output Feature Class: ... GWR4values.shp
Kernel Type: ADAPTIVE
Bandwidth method: BANDWIDTH_PARAMETER
Weights: Mudr_15y
Coefficient raster workspace: ... 2020 Census Tracts - Tabular
Leave all other fields blank or as filled by default
OK

Географически Взвешенная Регрессия, реализованная в ArcMAP10.x, дает три основных раздела: (А) общая диагностика, (Б) выходной класс объектов (шейп-файл), содержащий все локальные оценки, (В) растровые поверхности коэффициентов, отображающие каждый коэффициент отдельно.

Начнем с анализа дополнительной таблицы GWR_supp.dbf, в которой представлены основные результаты модели:

ACTION: Add GWR_supp to the TOC (*добавляем таблицу к Таблицы Слоев)
ArcCatalog >> Navigate to ....GWR4values_supp.dbf >> Drag and drop WR4values_supp.dbf to the TOC
TOC >> RC GWR_supp >> Open (* открываем таблице dbf по правому клику)

Интерпретация результатов Географически Взвешенной Регрессии проводится на фоне уже полученных показателей Метода Наименьших Квадратов, тем более что содержание статистик и их роль в описании успешности\неудачности модели нам известна. Проверим основные показатели.

Коэффициент Детерминации модели R2 = 0,966341 (0,875731 OLS)
Скорректированный Adjusted R-Squared = 0,944978 (0,875310 OLS)

Модель GWR объясняет около 95% вариации зависимой переменной, что на 7% выше (собственно R2 лучше на 9%. Ликвидация двух вроде значимых переменных только оптимизировала модель). Акайке критерий (AICc) равен 57,17 (6913,2 OLS) - в этом важном показателе мы значительно улучшили модель.


Рис. 6.23 Основные результаты модели GWR GWR_supp.dbf

Проверим Отображение стандартизированных остатков (Выходной класс объектов шейп-файла):

ACTION: Add GWR_supp to the TOC (*добавляем шейм стандартизированных остатков к таблице слоев)
ArcCatalog >> Navigate to ....GWR4values.shp >> Add to Display
TOC >> GWR4values.shp >> Open (*открываем шейп-файл).

Сравним распределение остатков для OLS и GWR


Рис. 6.24 Картограммы стандартизированных остатков OLS и GWR

Вспоминаем, что стандартизированные остатки показывают, какая часть вариаций пространственных данных не объясняется независимыми переменными. Как можно видеть на Картограмме GWR завышенные (синие) и заниженные (красные) остатки не образуют выраженных кластеров, и в целом их распределение выглядит в большей (чем на OLS) мере случайным. Таким образом, использование Географически взвешенной регрессии позволяет оптимизировать модель и в отношении стандартизированных остатков.

Регрессионный анализ, используемый для выявления зависимостей между изучаемым феноменом и объясняющими переменными - нетривиальная процедура, требующее терпения и экспертных решений практически на каждом шагу. Сила алгоритма - в неплохо отработанных и более-менее ясно интерпретируемых этапах. Основная слабость Регрессионного анализа заключается в том обстоятельстве, что линейные зависимости сравнительно редко встречаются как в природных, так и социальных процессах и явлениях. Поэтому в последние годы в самых разных сферах геопространственного анализа создаются специальные инструменты для исследования сложных нелинейных зависимостей.