III. ГЕОМОРФОМЕТРИЯ И СОВРЕМЕННЫЕ ПОДХОДЫ К ЛАНДШАФТНОМУ СИНТЕЗУ

13. СЛОЖНЫЕ АЛГОРИТМЫ СЕГМЕНТАЦИИ РЕЛЬЕФА

13.1. Поколение новых моделей 13.2. Классификации рельефа с использованием нечеткой принадлежности и нечеткого наложения 13.3. Методы сегментации рельефа, основанные на алгоритмах кластерного анализа 13.4. Методы "машинного" обучения и нейронные сети в классификации рельефа

III. ГЕОМОРФОМЕТРИЯ И СОВРЕМЕННЫЕ ПОДХОДЫ К ЛАНДШАФТНОМУ СИНТЕЗУ

13. СЛОЖНЫЕ АЛГОРИТМЫ СЕГМЕНТАЦИИ РЕЛЬЕФА

13.1. Поколение новых моделей

После того, как в геоморфометрии и ГИС-моделировании были разработаны метрики, позволяющие учитывать относительное местоположение на склоне, например, такие как Topographic Position Index|Индекс топографической позиции, Valley Depth|Глубина Долин, Height Above River|Высота над Уровнем Рек и др., появился целый ряд «прорывных» алгоритмов [Evans, Hengl, Gorsevski, 2009], [Evans, 2012], которые можно назвать моделями катенарно-гребне-килевой дифференциации.

После добавления к этим моделями «третьего измерения» в виде семейства параметров кривизны [Шарый, 2006], [Флоринский, 2016], возникла возможность наглядно презентовать трехмерные свойства местоположений (геотопов по Н.А.Ласточкину [Ласточкин, 1987]) как в широком геоморфологическом (мезоформы рельефа - landform), так и в более специальном (ландшафтные местоположения - landscape site) значении.

Широкое увлечение геоморфометрическими моделями [Geomorphometry..., 2009] привело сначала (в первое десятилетие нового века) к неоправданному оптимизму и убеждению, что моделировать можно все что угодно, которые по прошествии времени и накоплении опыта сменились скепсисом. Однако, обнаруженные недостатки новых моделей с точки зрения теории оказались не менее интересными, чем безусловные достижения и полученные результаты.

Первый недостаток, или, вернее - затруднение, заключалось в раскрывшейся (в ходе моделирования) неопределенности, казалось бы, устоявшихся географических понятий, прежде всего - геоморфологических, таких как "гора", "равнина", или "крутой", "пологий" и т.д. В моделировании задействуются, как правило, предварительно классифицированные тематические растры: в самом простом примере с рельефом, это означает, что, вводя в модель параметры высоты и крутизны мы должны определиться с таксонами «низкий-высокий», и «пологий-крутой». Однако выяснилось, что используемые в традиционной географии классификаторы, зачастую, локально некорректны и не универсальны в целом. Как мы уже убедились переменная абсолютная высота земной поверхности, а, следовательно, и производные от нее показатели не подчиняются гауссову распределению; включение в модель нескольких ненормально распределенных параметров сильно осложняет последующую классификацию любых интегральных таксонов. Для преодоления этих сложностей были разработаны модели, учитывающие Fuzzy Membership|Нечеткую Принадлежность (скажем, в виде правила «только 75% поверхностей с высотой более 500 м – «горы») и реализующие процедуры Fuzzy overlay|Нечеткого наложения.

Второе затруднение связано с попытками избежать зависимости результатов от масштаба моделирования и «зернистостью» исходных данных, которая не позволяла передавать важнейшие свойства иерархичности и фрактальности природных структур, что достигается посредством внедрения мультимасштабных алгоритмов, реализующих процедуру изменения размера расчетного «окна» "на лету" параллельно изменению размерности субстрата [Jasiewicz, Stepinski, 2013].

Известный прогресс был достигнут на новом уровне, однако, (как это всегда бывает в науке) разрешение одних проблем вывело на повестку дня другие. В частности, нерешенными остались вопросы об объективной (т.е., независимой от мнения эксперта) размерности иерархических пространственных уровней дифференциации, и оптимальных алгоритмах нечеткого наложения.

Отмеченные выше затруднения отчасти обусловили спрос на "почти" автоматизированные методы (сводящие участие эксперта, казалось бы, к минимуму), среди которых наибольшее применение обрели алгоритмы кластерного анализа, представляющие собой способ автоматической классификации ("группирования", "сегментации", "стратификации", "таксономии") сущностей в многомерном пространстве факторов и позволяющие разбивать совокупность объектов на группы по некоторому набору признаков (переменных). Методы кластеризации делятся на алгоритмы, предполагающие предварительное знание числа и характеристик итоговых классов - k-means кластеризация, дискриминантный анализ, деревья классификации и алгоритмы, в которых свойства итоговых таксонов неизвестны, а их число известно лишь предположительно - изокластерный анализ, анализ группирования.

Кластерный анализ применяется сегодня для решения широкого круга задач – от моделирования природных зон, до почвенного или ландшафтного картографирования, а также районирования и зонирования разного вида; можно сказать, что мы прибегаем к кластеризации, когда не очень хорошо представляем какие качества (признаки) объектов позволяют их классифицировать (или «группировать»), или когда таких признаков слишком много, либо они гетерогенны и сложно распределены.

Объективные преимущества такого подхода: возможность исследования сложных феноменов в многомерном пространстве ординации путем одновременной обработки практически любого числа переменных-факторов. Сложности – в сохраняющейся несмотря на "автоматизм") зависимости результата от решений эксперта, которые здесь распространяются, прежде всего, на число выходных классов, дистанцию соседства, размерность кластеров, локализацию затравок-образцов.


13.2. Классификации рельефа с использованием нечеткой принадлежности и нечеткого наложения

Одна из проблем моделирования ландшафтной дифференциации заключается, с одной стороны - в необходимости предварительного классифицирования используемых тематик (растров факторных переменных), с другой – в относительности (региональной пригодности) любых жестко закрепленных градаций: высотных градиентов («поясов»), уклонов и т.д. Принятие и использование алгоритмов нечеткой классификации для обнаружения элементов рельефа позволило использовать принципиально новые инструменты моделирования [Petry, Robinson, Cobb, 2005].

Теория нечетких множеств представляет собой альтернативный подход к классической теории множеств, который используется во многих областях науки в том числе в геоморфометрии и ландшафтной экологии. Существует два основных способа определения условий так называемой Fuzzy Membership|Нечеткой Принадлежности. Первый способ опирается на экспертные знания и часто упоминается как модель семантического импорта (SI), второй способ называется модельным подходом отношения сходства» (SR) и основывается на идентификации и характеристики кластеров данных. Нечеткие множества, генерируемые для различных переменных на основе ЦМР, а также нечеткие наложения переменных, часто обеспечивают удовлетворительные и выразительные модели местности [MacMillan, 2009].

К полуавтоматическим классификациям, использующим алгоритмы нечеткой принадлежности (нечеткого множества - Fuzzy Membership) могут быть отнесены:

Curvature Classification,
TPI Based Landform Classification,
Fuzzy Landform Element Classification.

Мы продемонстрируем эти алгоритмы на примере горной территории Приэльбрусья с помощью программного пакета SAGA GIS, в котором они были впервые реализованы (в настоящее время можно пытаться запускать эти же скрипты в ArcMAP10.x и QGIS, предварительно добавив их к набору инструментов).

Curvature Classification (Terrain Analysis>>Morphometry) - алгоритм классификации рельефа, основанный на сочетании различных видов параметров кривизны. Критическая опция диалога: выбор профильной (возможные варианты - Profile Curvature, Longitudinal Curvature) и плановой кривизны (варианты - Tangential Curvature, Cross-Sectional Curvature) [MacMillan, Shary, 2009]. Для Приэльбрусья применены опции:

Vertical Curvature: Profile curvature,
Horisontal Curvature: Tangential Curvature,
Treshhold Raius|Пороговый радиус: 50000,
Smoothing/Генерализация: 5.



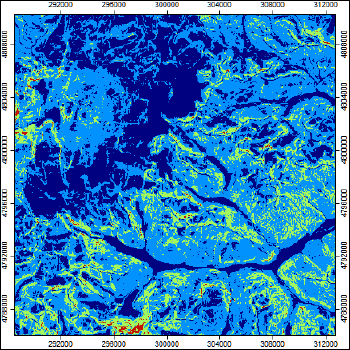
Рис. 13.1 Результат классификации рельефа методом Curvature Classification: X - выпуклые, V - вогнутые; легенда: X|X - привершинные поверхности, GE|X - верхние части склонов, V|X - средние части склонов, X|GR - нижние части склонов, GR|GE - плоскость, V|GR - верховья и "третьи склоны" ложбин, X|V - средние звенья эрозионной сети, GE|V - днища долин, V|V - русловые элементы и замкнутые понижения

На выходе классификации Curvature Classification 8 мезоформ рельефа, индексированная посредством ссылки на форму склонов в плане и профиле (Рис. 13.1).

Curvature Classification|Классификация по Кривизне поверхности хорошо отражает пластику холмистого рельефа; однако в горах, где широко распространены прямые фрагменты и фасеты склонов алгоритм "отбивает" привершинные (и пригребневые) условно плоские поверхности, а также днища более-менее широких ущелий. Остальная территория дробится на фрагменты склонов, различающихся по положению (верхние, нижние) и крутизне. Комплементарная пригребневым (т.е., хребтам и контрфорсам) прикилевая эрозионная система с желобами вдоль склонов, распадками между склонами, и ущельями между хребтами, сохраняет целостность отображения лишь частично. Результат можно диверсифицировать и оптимизировать (до какой-то степени), выбирая иные виды кривизны (в позициях Vertical Curvatue и Horizontal Curvature) и меняя показатель Smoothing, регулирующий уровень генерализации модели.

Следующий алгоритм классификации с использованием нечеткой принадлежности, реализованный в SAGA GIS - Fuzzy Landform Element Classification (Terrain Analysis>>Morphometry) представляет собой делимитацию форм рельефа (landform) по уклону и нескольким другим параметрам, используемым в качестве входных данных для неконтролируемой классификации (например, ISODATA или k-means).

Моделирование включает два этапа. На первом рассчитываются три параметра, описывающие относительную неопределенность классификации: Maximum Membership|Максимальная принадлежность, Entropy|Энтропия, и так называемый Confusion Index|Индекс конфузии» значений. На втором этапе выделяются собственно местоположения.

По умолчанию в позиции Imput диалогового окна в качестве второй метрики выставлена абсолютная высота Elevation, однако алгоритм выдает более адекватный результат для варианта slope and curvatures, позволяющего привлечь к анализу четыре вида кривизны: Minimum Curevature|Минимальная Кривизна, Maximum Curvature|Максимальная Кривизна, Proftle Curvature|Профильная кривизна, Tangetnial Curevature|Тангенциальная кривизна.


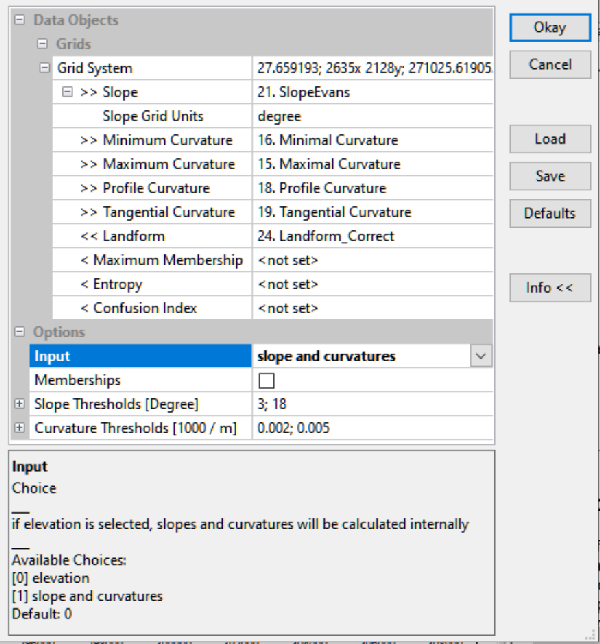
Рис. 13.2 Диалоговое окно инструмента Fuzzy Landform Element Classification SAGA GIS

Первичные метрики кривизны должны быть предварительно построены в SAGA GIS (инструмент Slope, Aspect, Curvature); также необходимо выявить пороговые значения крутизны склонов и кривизны через условное (в изображении) классифицирование - это делается простым нажатием на слой в таблице данных Data>>RC>>Classify.

Дефолтные пороговые значения Slope|Уклона: 50 и 150. Это означает, что «плоская поверхность» имеет уклон менее 50 (принадлежность slope=0), а поверхность с крутизной более 150 отнесена к «склону» (принадлежность slope=1); тогда как значения в промежутке между этими пороговыми значениями (50 < slope < 150) дают дробное значение принадлежности между 0 и 1. Например, если уклон местности 70, то вероятность отнесения ее к категории "плоскость"равна 0,8 (или 80%), а вероятность отнесения к категории «склон» соответственно 0,2 (20%). В настройках Fuzzy Landform Element Classification по умолчанию в позиции Slope Treshhold (Degree)|Пороговое значение уклона (градусы) выставлено 2, 7 - параметры, подходящие скорее для холмистой местности, но не для высокогорья Северного Кавказа. В нашем случае применяем 3, 18 соответственно.


Рис. 13.3 Классификация уклона для выявления граничных значений "плоскости" и "склона"

Таким же образом, следует ориентироваться на значения Total Curvature, чтобы корректно установить опцию Curvature Threshold; по умолчанию здесь выставлены Пороговые значения кривизны: 0.000002; 0.00005 - которые следует воспринимать как "нулевые", т.е., указывающие на отсутствие кривизны, и доминирование рельефа, как бы набранного из плоскостей (фасеты и фрагменты склонов). Эти величины затем используются для вычисления вероятности того, что любое заданное значение попадает в диапазон значений вертикальной и горизонтальной кривизны для различных типов кривизны (например, минимальная, профильная и т. д.). Математика здесь достаточно проста; Пороговые значения кривизны, установлены исходя из характерных для рельефа и будут варьироваться в зависимости от типа характеризуемой местности: "переломные" значения Total Curvature выставляем ориентируясь на полученные предварительной классификацией этой переменной - 0.002 и 0.005 соответственно.


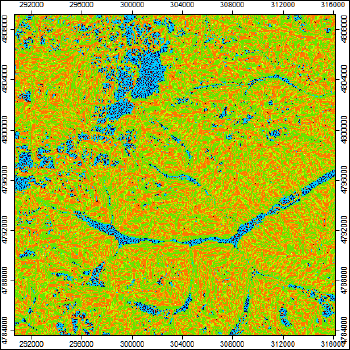
Рис. 13.4 Классификация мезоформ Приэльбрусья на основе нечеткой принадлежности

Результатом применения алгоритма Fuzzy Landform Element Classification являются 15 классов «формообразующих элементов» для понимания которых следует ориентироваться на матрицы комбинаций кривизны (см. раздел 11.1, Рис. 11.3).


Таблица 13.1 Типология элементарных поверхностей Fuzzy Landform Element Classification
Привершинные/принизинные ЭП (макс-мин кривизны) Пригребневые ЭП (горизонтальная-профильная кривизны) Склоновые ЭП (горизонтальная-профильная кривизны) Прикилевые ЭП (горизонтальная-профильная кривизны)
Peak|Пик выпукло-выпуклая привершинная ЭП "X/X" Nose|Плечо выпукло-выпуклая ЭП "X/X" Shoulder slope|Плечо склона выпуклая по профилю, прямая в плане склоновая ЭП "X/S" Hollow shoulder|Выпуклая ложбина вогнутая в плане, выпуклая по профилю ЭП "X/V"
Plain|Плато (равнина) плоская привершинная ЭП "S/S" Spur|Контрфорс прямо-выпуклая ЭП "S/X" Planar slope|Простой склон, прямая в плане и в профиле склоновая ЭП "S/S" Hollow|Вогнутая ложбина прямая по профилю вогнутая в плане ЭП "S/V"
Saddle|Седло выпукло-вогнутая килевая привершинная ЭП "X/V" Spur foot|Подножье гребня вогнуто-выпуклое "V/X" Foot slope|Подножье склона вогнутое по профилю прямое в плане ЭП "V/S" Hollow foot|Вогнутая по профилю концентрирующая вогнутая в плане ложбина ЭП "V/V"
Ridge|Пригребневая выпукло-плоская ЭП "X/S" --- --- ---
Channel|Трог плоско-вогнутая ЭП "S/V" --- --- ---
Pit|Замкнутая депрессия вогнуто-вогнутая ЭП "V/V" --- --- ---
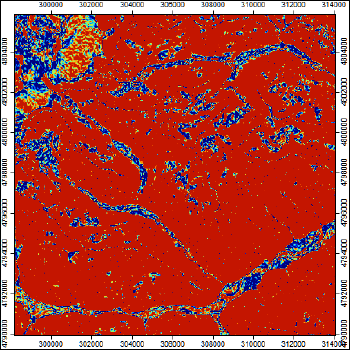
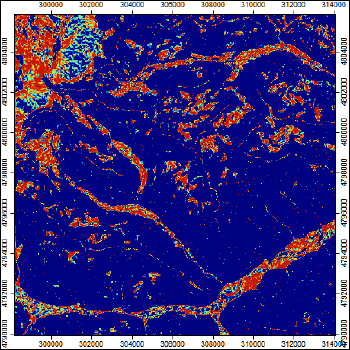
* Примечание: S - прямые элементы, значение кривизн - 0, X - выпуклые элементы - значение кривизн +1, S - вогнутые элементы, значения кривизн - -1

"Побочным" продуктом алгоритма Fuzzy Landform Element Classification являются три дополнительных растра, позволяющие лучше оценить результаты моделирования: Maximum Membership|Максимальная принадлежность, Entropy|Энтропия, Confusion Index|Индекс неопределенности.


Рис. 13.5 Дополнительные растры - результат Fuzzy Landform Element Classification: a) Растр Maximum Membership|Максимальная принадлежность, b) Entropy|Энтропия

Максимальная принадлежность характеризует надежность отнесения пикселя грида к тому или иному классу, можно убедиться, что она высока (около 0,9) для большей части сравнительно простых по форме склонов, и, напротив, низка (менее 0,7) для прикилевых форм и участков пойм и днищ ущелий. Соответственно противоположным образом распределена Энтропия, максимальные значения которой (около 0,2) приходятся на днища долин и склоны сложных форм.

Еще один алгоритм, построенный на нечеткой логике и весьма популярный среди исследователей - TPI Based Landform Classification|Классификация мезоформ на основе индекса Топографической позиции - широко используется при моделировании прогнозных|predictable почвенных и ландшафтных карт.

Topographic position index (TPI)|Индекс топографической позиции – переменная второго порядка, позволяющая различать местоположения вдоль катены: от привершинных (пригребневых) ЭП до подножий склонов и прикилевых элементов эрозионной сети [Wilson, Gallant. 2000]. A. Weiss [Weiss, 2001] предположил, что значения TPI, полученные для разных размеров «скользящего окна» (т.е., в разных масштабах), могут использоваться для создания классификации местности или категоризации объектов и форм рельефа в пределах ландшафта. О. Конрад (O. Conrad) в рамках SAGA GIS разработал алгоритм, позволяющий сначала получить два разномасштабных индекса TPI, а затем комбинировать их классифицированные растры.

Диапазоны значений TPI могут использоваться для категоризации объектов и форм рельефа и классификации ландшафтных местоположений. Важно помнить, что TPI зависит от масштаба; это означает, что размер и форма фокальной области, выбранной для расчета начальных значений, могут выделять или игнорировать те или иные элементарные поверхности.

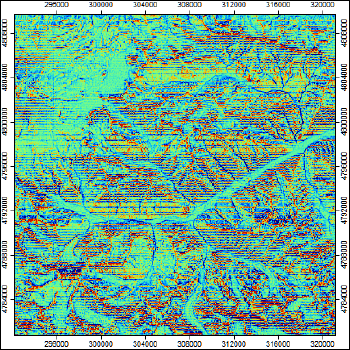
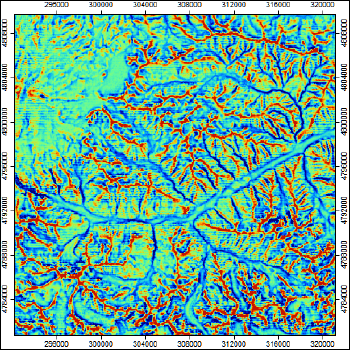
До использования алгоритма имеет смысл получить несколько растров Topographic Position Index (TPI) с разными соотношениями Кернель-радиуса (позиция Scale), и вариантами учета расстояний (Weighting Function)


Рис. 13.7 Разномасштабные Индексы топографической позиции с соотношением "окон": a) 0-100, b) 30-300, c) 30-1000

Значения TPI изменяются от положительных (максимально +2), соответствующих привершинным и пригребневым местоположениям до отрицательных (-2), отображающих килевые (поймы, ложбины. лощины) местоположения. Между этими значениями - верхние, средние и нижние участки склонов.

На примере ключевого участка Приэльбрусья (Рис. 13.7) можно убедиться, что при небольших (по умолчанию 0-100) значениях окна алгоритм выявляет локальные вогнутые и выпуклые перегибы рельефа таким образом, что в пределах долин можно различать тыловые швы и днища (поймы), но остальные элементы гребне-килевой дифференциации разбиваются на множество отдельных фасет, что искажает реальную картину. Изменение порогового значения первого (меньшего) окна позволяет (30-300) выделить более цельно систему пригребневых поверхностей. Для горных территорий может оказаться полезным учесть функцию расстояний как экспоненту (exponential).

Алгоритм TPI Based Landform Classification хорошо «различает» элементы гребне-килевой дифференциации, но итоговый растр предстает в «едином» масштабе без выявления иерархии форм, что отчасти объясняется использованием только двух масштабных окон анализа. Метод широко используется на локальном уровне, в частности для построения камеральных (гипотетических) почвенных карт, поскольку позволяет учесть различия в режимах (элювиальный, транзитный, аккумулятивный) почвообразования.


Рис. 13.8 Классификация мезоформ территории Приэльбрусья на основе разномасштабных индексов топографической позиции

На выходе модели - 10 условных форм рельефа:

  1. High Ridges - высокие хребты,
  2. Midleslope Ridges - средневысотные хребты,
  3. Local Ridges локальные боковые гребни (контрфорсы),
  4. Upper Slope - верхние части склонов,
  5. Open Slope - нижние части склонов,
  6. Plains - равнинные участки,
  7. Valleys - долины,
  8. Upland Drainages - верхние элементы ложбинно-лощинной сети,
  9. Midleslope Drainages средние участки долин,
  10. Streams - русла, конкретные параметры которых будут зависеть от используемой ЦМР и входных опций.

13.3. Методы сегментации рельефа, основанные на алгоритмах кластерного анализа

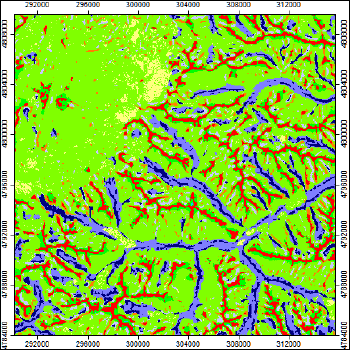
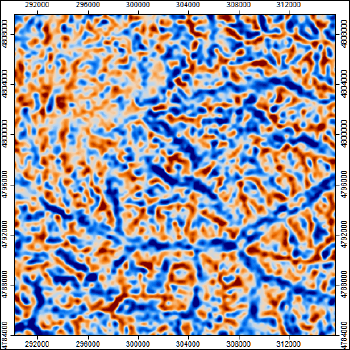
Учет смежных элементов мезорельефа – единственный способ выявления исчерпывающей характеристики местоположения. Мысль о необходимости учета общего характера поверхности для корректной дифференциации отдельных местоположений получила развитие в некоторых алгоритмах геоинформационного моделирования рельефа. Один из них – алгоритм Terrain Surface Classification, предложенный Дж. Ивахаши и Р. Пайком [Iwahashi, Pike,2007] и реализованный в SAGA GIS, предусматривает предварительный расчет так называемой текстуры (Texture), выпуклости (Convexity) и уклона Slope.

Terrain Surface Convexity (Terrain Analysis>>Morphometry) - сложная переменная, расчет которой предложен теми же авторами и реализован О. Конрадом (2015). Перевод этого свойства как "выпуклость" не исчерпывает вполне его содержания, можно лишь констатировать что Convexity еще один способ отражения гребне-килевой и склоновой дифференциации поверхности. Использование инструмента предполагает сразу несколько критических настроек, заметно влияющих на итоговый растр. Прежде всего это Laplacian Filter Kernel - инварианты соседства ячеек расчетного окна:

  • conventional four-neighborhood|четыре ячейки по сторонам,
  • conventional eight-neighborhood| восемь ячеек, четыре по сторонам и четыре по угла
  • eight-neighborhood distance based weighting|восемь со взвешенным расстоянием.

Вторая важная настройка Flat Area Threshold|Пороговое значение уклона плоской поверхности с дефолтным значением 0o, подходящим только для равнинных территорий, в горах его следует поднять по крайне мере до 3o. Можно также поэкспериментировать с масштабом расчета Scale, который выражается в числе ячеек (дефолтное значение 10). Критически важна опция Method, предлагающая выбрать между resempling|посев образцов и counting cells|выбор по значению ячеек. Может оказаться небесполезным экспериментирование с опцией Weighting function|Тип взвешивания расстояния, в том случае если в позиции Laplacian Filter Kernel было выставлено значение eight-neighborhood distance based weighting|восемь со взвешенным расстоянием, наконец, чтобы конкретизировать этот вариант в последней позиции следует указать величину Brandwidth, если "взвешивание" расстояния производится по экспоненциальной функции (значение по умолчанию 0,7, может быть изменено в диапазоне от 0,00 до 1,00).


Рис. 13.9 Terrain Surface Convexity для территории Приэльбрусья

Низкие значения (< 36) Convexity маркируют днища долин и ущелий, высокие (> 60) - гребни хребтов и контрфорсы, между крайними значениями можно зафиксировать различные (верхние и нижние) части склонов. Растр Convexity позволяет фиксировать и замкнутые понижение в высокогорье, которые могут быть ассоциированы с полуцирками, или верхними "тыловыми" частями склонов.

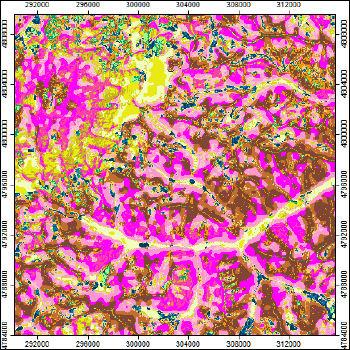
Инструмент Terrain Surface Texture имеет аналогичные опции настройки. Все три растровых файла Convexity, Texture, SLope заводятся вместе с основным файлом Elevation как входные для алгоритма Terrain Surface Classification. Все опции настройки дублируют таковые для переменной Convexity: Number of Classes|Число классов, Scale|Масштаб, Laplacian Filter Kernel (определение модели соседства ячеек в расчетном окне), пороговое значение плоскости Flat Area Threshold, - логично их воспроизвести и в этом скрипте.

Terrain Surface Classification дифференцирует рельеф на число классов, кратное четырем - 8, 12 или 16, и которые интерпретируются как склоны различной крутизны, фрагментированности и выпуклости/вогнутости.


Рис. 13.10 Terrain Surface Classification - классификация форм земной поверхности

  1. very steep slope, fine texture, high convexity|верхние привершинные части круто-выпуклых рассеивающих склонов хребтов;
  2. very steep slope, coarse texture, high convexity|круто-выпуклые протяженные средние части склонов;
  3. very steep slope, fine texture, low convexity|верхние части прямых склонов хребтов;
  4. very steep slope, coarse texture, low convexity|нижние части слабо-выпуклых рассеивающих склонов;
  5. steep slope, fine texture, high convexity|небольшие фрагменты покато-выпуклых склонов;
  6. steep slope, coarse texture, high convexity|крупные покато-выпуклые склоны
  7. steep slope, fine texture, low convexity|небольшие фрагменты привершинных крутых прямых склонов;
  8. steep slope, coarse texture, low convexity|крупные участки крутых почти прямых склонов;
  9. moderate slope, fine texture, high convexity| крупные почти прямых нижних (приложбинных и придолинных) склонов;
  10. moderate slope, coarse texture, high convexity|небольшие участки пригребневых седловидных поверхностей;
  11. moderate slope, coarse texture, high convexity|крупные участки полого-выпуклых склонов;
  12. moderate slope, fine texture, low convexity|периферийные части замкнутых понижений;
  13. gentle slope, coarse texture, low convexity|склоны вторичных хребтов и контрфорсов;
  14. gentle slope,fine texture, high convexity|верхние (тыловые) части ложбин и полуцирков<;/li>
  15. gentle slope, fine texture, low convexity|замкнутые понижения днищ долин и пойм, депрессии полуцирков;
  16. gentle slope, coarse texture, low convexity|слабо-наклонные плато и днища долин (ущелий), поймы рек.

На территории Приэльбрусья алгоритм хорошо выделяет пригребневые поверхности, объединяя их систему основных хребтов с боковыми отрогами, а также контрфорсы и уступы; неплохо вычленяются и элементы эрозионной и долинно-речной сети. Однако, в предгорьях и на равнинах пластика форм, отображаемая этим алгоритмом не так наглядна, поскольку не вполне корректно «отбиваются» уступы субгоризонтальных поверхностей. Вполне вероятно, что опции для условных "гор" и "равнин" не могут быть выбраны корректно в пределах единой сцены, в этом случае естественным решением будет раздельное моделирование для горной системы и предгорной равнины.


Рис. 13.11 Terrain Surface Classification - детализированное 3D изображение

Другие недостатки проявляются при попытке интерпретации и детальном анализе результата. Во-первых, классификация "теряет" пространственную связь между элементарными поверхностями как по профилю (на катене), так и в плане. Последовательность номеров классов в этом отношении не должны вводить в заблуждение: таксоны сгруппированы по крутизне (очень крутые - крутые - покатые - пологие и плоские), дальнейшее различение осуществляется по крупности элемента (coarse-fine) и "выпуклости". Во-вторых, характеристики профильной кривизны сведены только к мере "выпуклости", в итоге прямые и вогнутые склоны завуалированы как "слабовыпуклые", что затрудняет выделение килевых ЭП (например - элементов ложбинно-лощинной сети). В-третьих, классификация не содержит указаний на относительную высоту: одни и те же элементы (например 11,12,14) могут располагаться как на привершинной поверхности (на гребне или вершине горы), так и в пределах долин (поймы, террасы) или полузамкнутых понижений (цирков и полуцирков между вершинами).

Таким образом, алгоритм позволяет в общих чертах зафиксировать гребне-килевую дифференциацию (основные хребты и боковые гребни - таксоны 1,3,5), катенарную дифференциацию (5,6,4,8), а также прикилевые ЭП (днища долин - 16, тыловые швы - 14, углубления низких пойм - 15), наконец - замкнутые понижения различного генезиса на склонах (9,11). Тем не менее, результат вполне можно рассматривать как "полуфабрикат" который может быть усовершенствован за счет добавления параметров относительной высоты (например, Height above river) и формы склона (Plane Curvature).

Terrain Clustering - более сложный и совершенный алгоритм, реализованный в SAGA GIS (Tool Chains>>Terrain Analysis>>Terrain Clustering) предложен автором как "черный ящик" (O. Conrad, 2015), в котором пользователю предлагается выбрать только число классов и число итераций. Но если открыть скрипт в текстовом редакторе, то становится понятным, что перед нами - собой кластерный анализ с предварительным расчетом параметров Normalized Height|Нормализованной высоты, Aspect|Экспозиции, Slope|Уклона, Tangential curvature|Тангенциальной кривизны и Total Gaussian curvature|Полной Гауссовой кривизны, Positive Openness|Положительной и Negative Openness|Отрицательной топографической открытости.

Показатели так называемой Открытости|Openness" привлекаются в данном алгоритме для контроля над размерностью и конфигурацией расчетного "окна", которые как бы следуют за размерностью реальных форм рельефа [Anders et al., 2009]. Топографическая Открытость связана с тем, насколько обширное пространство может быть увидено с конкретной позиции, поэтому положительные значения открытости выражают доминирование точки над местностью, а отрицательные - напротив замкнутость и закрытость. Было доказано, что Топографическая открытость является возможным способом учета разномасштабных форм в геоморфологическом моделировании. Инструмент SAGA GIS Topographic Openness (Terrain Analysis>>Lighting, Visibility) позволяет моделировать одноименную переменную с учетом фрактальности (опция Method - multi scale) и в "одномерном" пространстве (line tracing) [Yokoyama et al., 2002].


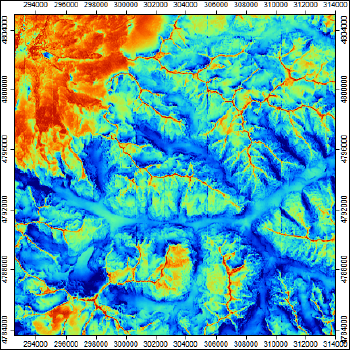
Рис. 13.12 Показатель Positive Openness - положительной топографической открытости для территории Приэльбрусья

Переменная Positive Openness позволяет выделить участки, видимые практически с любой точки - гребни и пригребневые поверхности высоких хребтов; склоны гор имеют средние значения, причем заметно различие между выпуклыми (более видимыми) и вогнутыми фрагментами. Характерно также что зоны "невидимости" значительно шире реальных границ небольших ущелий и распадков. На дне крупных долин невидимыми являются в основном тыловые части пойм и примыкающие к ним подножья крутых склонов; центральные части относительно открыты.


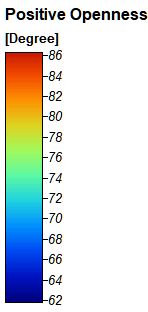
Рис. 13.13 Показатель Показатель Negative Openness - отрицательной топографической открытости для территории Приэльбрусья

Переменная Negative Openness не является простым "антиподом" положительной открытости и отличается более тонкой проработкой отрицательных форм рельефа, и, возможно, более адекватным представлением видимых привершинных областей.

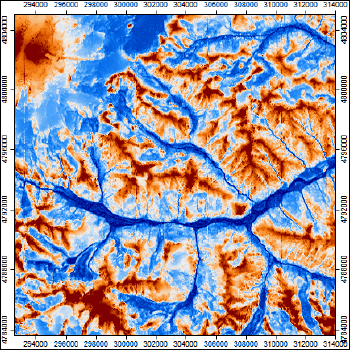
Terrain Clustering дифференцирует поверхность на кластеры, значения которых определяет пользователь, в этом еще одна особенность алгоритма.


Рис. 13.14 Terrain Clustering - 16 классов мезоформ рельефа для территории Приэльбрусья

Также, как и в предыдущем случае, номера таксонов Terrain Clustering условны, а их последовательность не отражает взаиморасположения в гребне-килевой и катенарной дифференциации, однако у эксперта всегда остается возможность переклассификации полученных таксонов и присвоения им необходимых индексов.


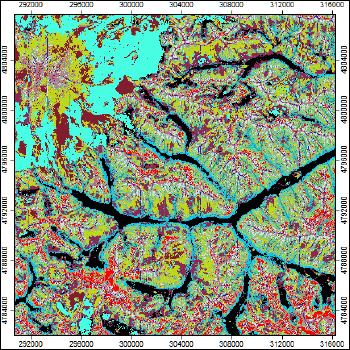
Рис. 13.15 Классы мезоформ рельефа - фрагмент 3D изображение

Интерпретация результата на ключевом участке (Рис. 13.14) может выглядеть следующим образом:

  • 1 - днища долин и ущелий (в том числе поймы),
  • 2 - выпуклые крутые верхние части пригребневых склонов,
  • 3 - крутые фасы склонов и скальные стенки,
  • 4 - плоские обширные, в том числе привершинные поверхности,
  • 5 - короткие фасы прямых привершинных склонов,
  • 6 - протяженные пологие нижние части склонов, рассеивающие,
  • 7 - пологие и полого-наклонные плато,
  • 8- локальные депрессии склонов,
  • 9 - желоба и кулуары, ложбины верхних частей склонов,
  • 10 - гребни хребтов и контрфорсов,
  • 11 - покатые и пологие слабовогнутые нижние части пригребневых склонов,
  • 12 - самые верхние привершинные части рассеивающих склонов,
  • 13 - бровки и уступы коренных склонов (и фрагментов террас) долин и ущелий,
  • 14 - прямые и слабо-вогнутые средние части пригребневых склонов,
  • 15 - протяженные лощины, распадки, желоба склонов.
  • 16 - плоские вершины и платообразные поверхности на разных топографических уровнях,

    • Алгоритм кластеризации может быть воспроизведен пользователем самостоятельно с предварительным моделированием необходимых метрик и последующим запуском инструмента K-Means Clustering for Grids (Imagery>>Classification): возможно это оптимальный путь, который позволяет варьировать состав метрик в зависимости от условий.

    K-Means Clustering for Grids - неконтролируемая классификация, основанная на K-средних алгоритме, определяющем центры кластеров и элементы, принадлежащие им, путем минимизации целевой функции, основанной на квадрате ошибок. Иными словами функция алгоритма заключается в том, чтобы расположить центры кластеров как можно дальше друг от друга и, одновременно, чтобы связать каждую точку данных с ближайшим центром кластера. Евклидово расстояние обычно используется в качестве меры несходства в алгоритме k-средних - порог, который обозначает наименьшее возможное значение расстояние для перемещения центров кластеров перед остановкой итерационного процесса [Jain, 2009].

    Набор переменных пользователь может выбирать по своему усмотрению исходя из характера местности, так для территории Армении апробировано сочетание Elevation, Flow Path Length|Длина Пути Потока, Plan Curvature, Profile Curvature, Slope [Piloyan, Konečný, 2017].

    Параметр Flow Path Length|Длина Пути Потока рассчитывается в SAGA GIS (Terrain Analysis>>Hydrology) и является еще одним показателем, используемым для конфигурирования матрицы водосборов а также для определения эрозионного потенциала территории. Этот инструмент вычисляет среднюю длину пути потока, начиная с "сеянных ячеек" (seeds) грида абсолютной высоты, которые либо задаются случайной предварительно сгенерированной сеткой (опция Seeds входных данных) либо извлекаются из вершин и гребней. Вторая критическая опция - Flow Routing Algorithm|Способ Маршрутизации Потока, в этой позиции можно выбрать Detervinistic D8|Детерминированный 8 (D8) [O'Callaghan, Mark, 1984], предполагающий расчет по восьми обычным румбам, либо Multiple Flow Direction|Множественное направление потока (FD8) [Quinn et al., 1991]. Последняя важная опция алгоритма - значение Convergence|Конвергенции (дефолтное - 1,1).


    Рис. 13.16 Flow Path Length - метрика Длины Пути Потока

    После определения набора входных растров в диалоговом окне инструмента кластеризации K-Means Clustering for Grids необходимо выбрать число итоговых выходных кластеров (т.е., число классов) и один из трех возможных алгоритмов: Hill Climbing [Rubin, 1967], Iterative Minimum Distance [Forgy, 1965]) или комбинированный способ Combined Minimum Distance/Hill Climbing. Разумеется, результат будет сильно зависеть от набора переменных, размерность которых может быть весьма различной (скажем, длина пути потока может достигать многих сотен метров, максимальный уклон в градусах не превышает отвесного угла в 90o, а различные виды кривизны изменяются в долях единицы), поэтому в алгоритме присутствует опция нормализации данных Normalise.


    Рис. 13.17 Неконтролируемая K-means кластеризации на 14 классов с пятью переменными

    Полезной особенностью метода является возможность получения таблицы статистики, дающей конкретное представление о характеристиках классов.


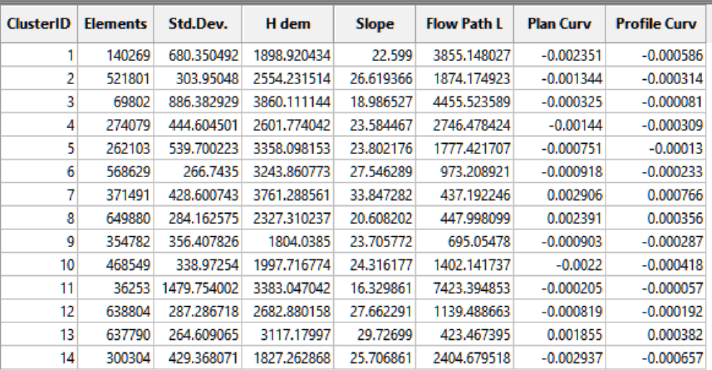
    Рис. 13.18 Скриншот таблицы статистики 14 классов итогового растра неконтролируемой кластеризации К-средних

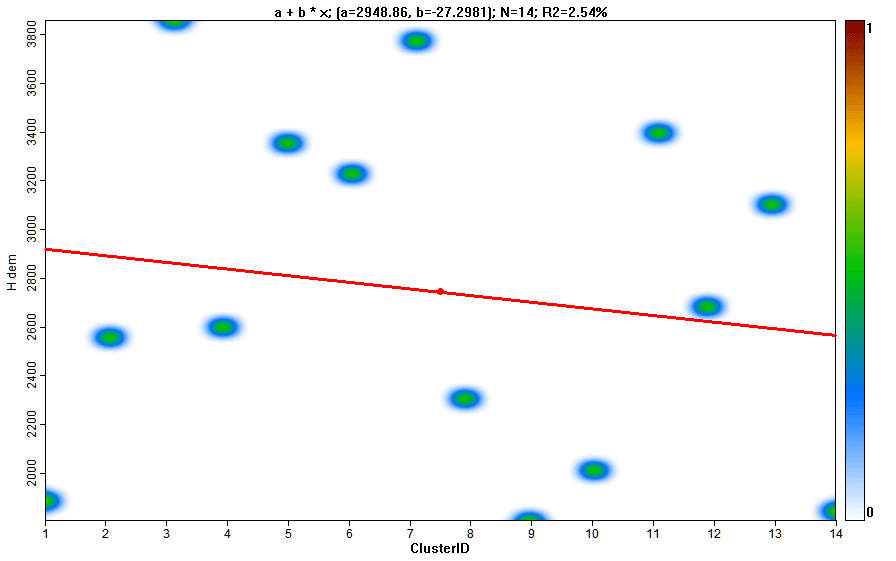
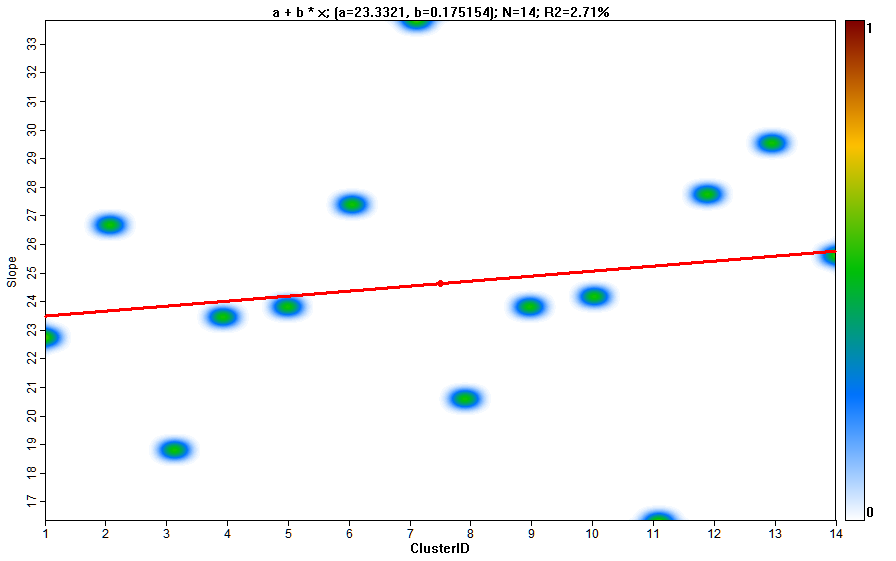
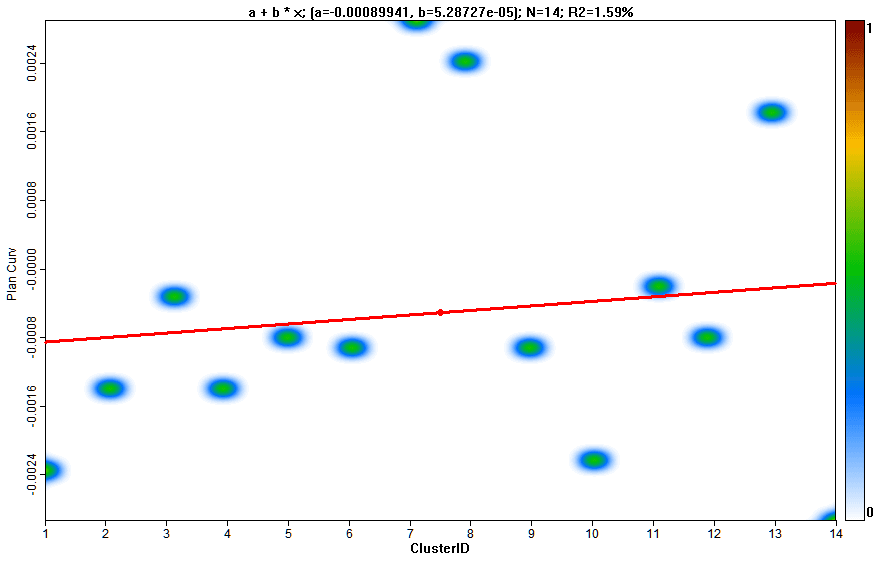
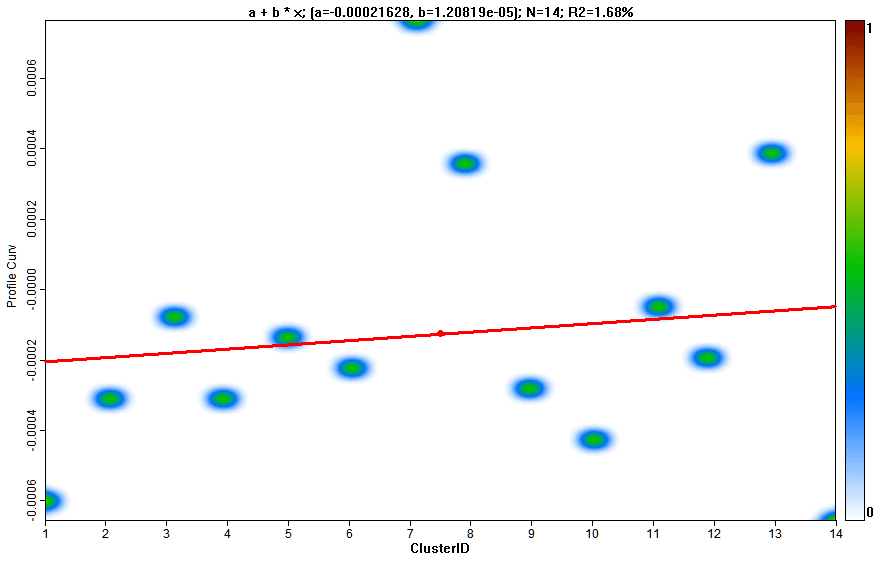
    В свою очередь таблица статистики может быть использована для построения графиков с характеристиками кластеров


    Рис. 13.19 Графики свойств кластеров: а) абсолютная высота, b) уклон, c) плановая кривизна, d) профильная кривизна

    В заключение обзора возможностей кластерного анализа для сегментации рельефа изменив набора переменных и введя в позиции Grids семь показателей: Normalized Height, Slope, Aspect, Tangential Curvature, Total Curvature, Positive Openness, Negative Openness.


    Рис. 13.20 Неконтролируемая K-means кластеризации на 16 классов с семью переменными (включая экспозицию)

    Как уже упоминалось выше результат кластеризации закономерно зависит от подбора факторов-переменных. Рисунки 13.20 и 13.21 демонстрируют эффект "выключения" всего одного фактора из набора - экспозиции. Очевидно, что в горах разнонаправленные склоны могут испытывать различный режим инсоляции, нагрева-охлаждения и увлажнения, поэтому этот фактор для горных территорий практически всегда значим.


    Рис. 13.21 Неконтролируемая K-means кластеризации на 16 классов с шестью переменными (без экспозиции)

    Кластерным анализом является и алгоритм Relief Segmentation (Tools>>Tool Chains), представляющий собой "серый ящик" (инструмент построен в Tool Chain SAGA GIS - аналоге Model Builder ArcMAP10.x), поскольку этапы расчета не раскрыты. Базовые метрики: Topographic Openness, Slope, Topographic Position Index, Topographic Wetness Index. Последовательность расчетов выглядит следующим образом (Relief Segmentation Tools, SAGA):

    1. Рассчитываются метрики Topographic Openness, Slope, TPI и TWI;
    2. Проводится анализ главных компонент (Principle Component Analysis);
    3. По результатам анализа главных компонент осуществляется посев стартовых точек (Seed points);
    4. На основании алгоритма "простого роста" строятся растровые ареалы;
    5. Проводится векторизация ареалов в полигоны и расчет статистики по каждому полигону;
    6. Проводится кластерный анализ на основании статистики;
    7. Полигоны сливаются (dissolve) по номеру кластера.

    Таким образом, специфика данного алгоритма - набор метрик (привлечение Индекса Топографической позиции Влажности) и использование процедуры Анализ Главных Компонент.


    Рис. 13.22 Relief Segmentation - кластеризации на 16 классов для ключевого участка Приэльбрусья

    Алгоритм Relief Segmentation неплохо справляется с выделением привершинных местоположений, не разрывает и показывает днища и террасы крупных долин (отображены даже отдельные фрагменты пойм), сохранена целостность и иерархия вторичных боковых притоков, отдельно выделились расширенных верховья горных долин в виде расширенных языковидных форм, "перепиливающих" гребни хребтов.


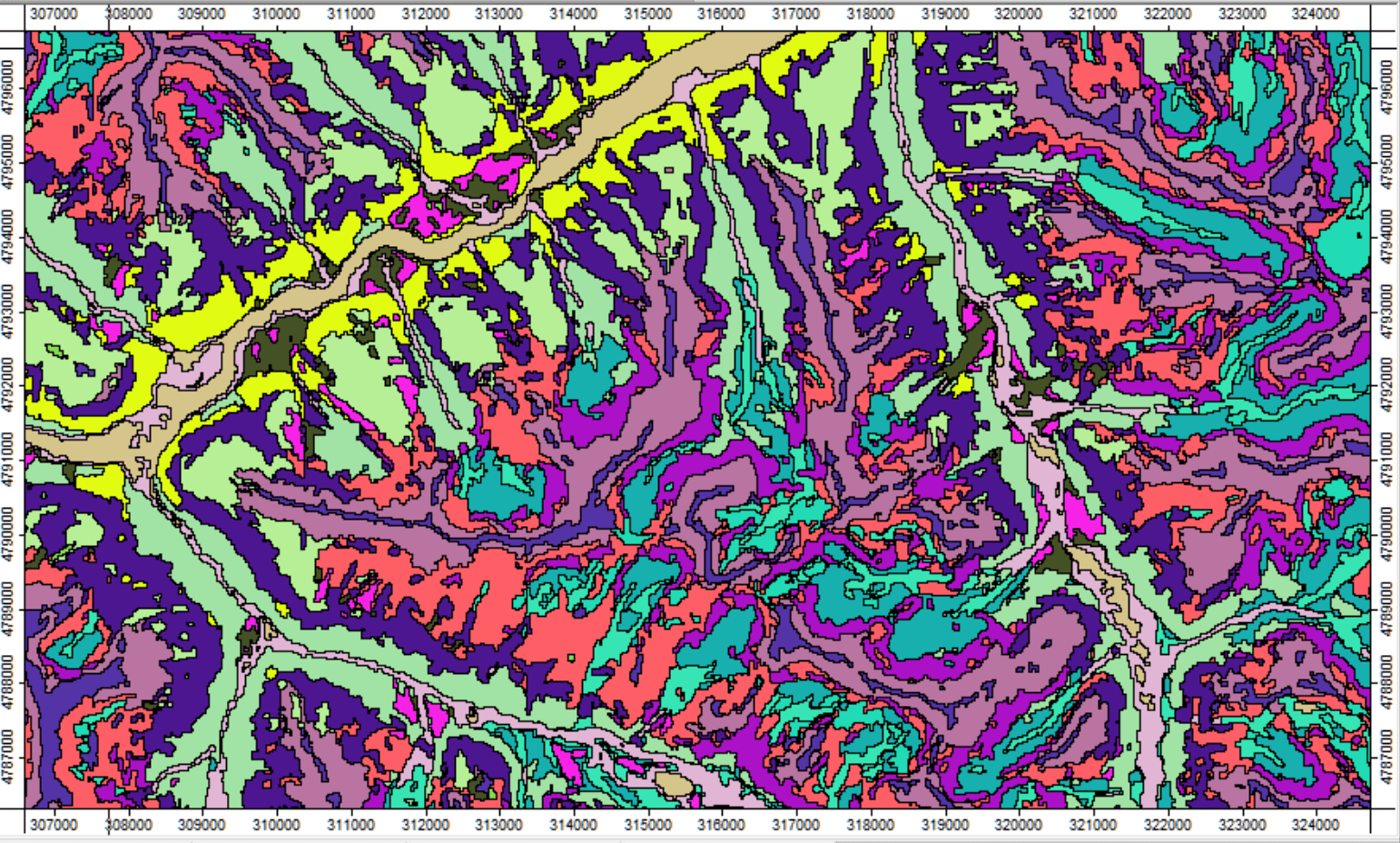
    Рис. 13.23 Relief Segmentation - кластеризации на 16 классов (фрагмент)

    Неплохо передана и структура главных хребтов: узкие гребни, примыкающие к ним крутосклонные скальные стенки, концентрирующие вогнутые в профиле и плане листовидные элементарные водосборы, и рассеивающие выпуклые участки склонов по обе стороны от контрфорсов.

    Метод (при условии настройки) неплохо справляется с холмистыми территориями и среднегорьем. Поскольку в кластеризации участвуют сразу два индекса, характеризующие положение точки на склоне (TPI) и относительно эрозионно-русловой сети (TWI) критическую роль играет настройка соотношения двух масштабных окон (значение по умолчанию 100, 1000), небезразличны к результату и опции Number of Clusters|Число Кластеров а также дистанция посева первоначальных точек Band Wind. В качестве примера приведем более-менее удачно подобранных опций приведем пример классификации форм рельефа для территории природного парка Ергаки (Рис. 13.24) с хорошо отображенными двумя комплементарными и иерархически дифференцированными системами хребтов и долин.


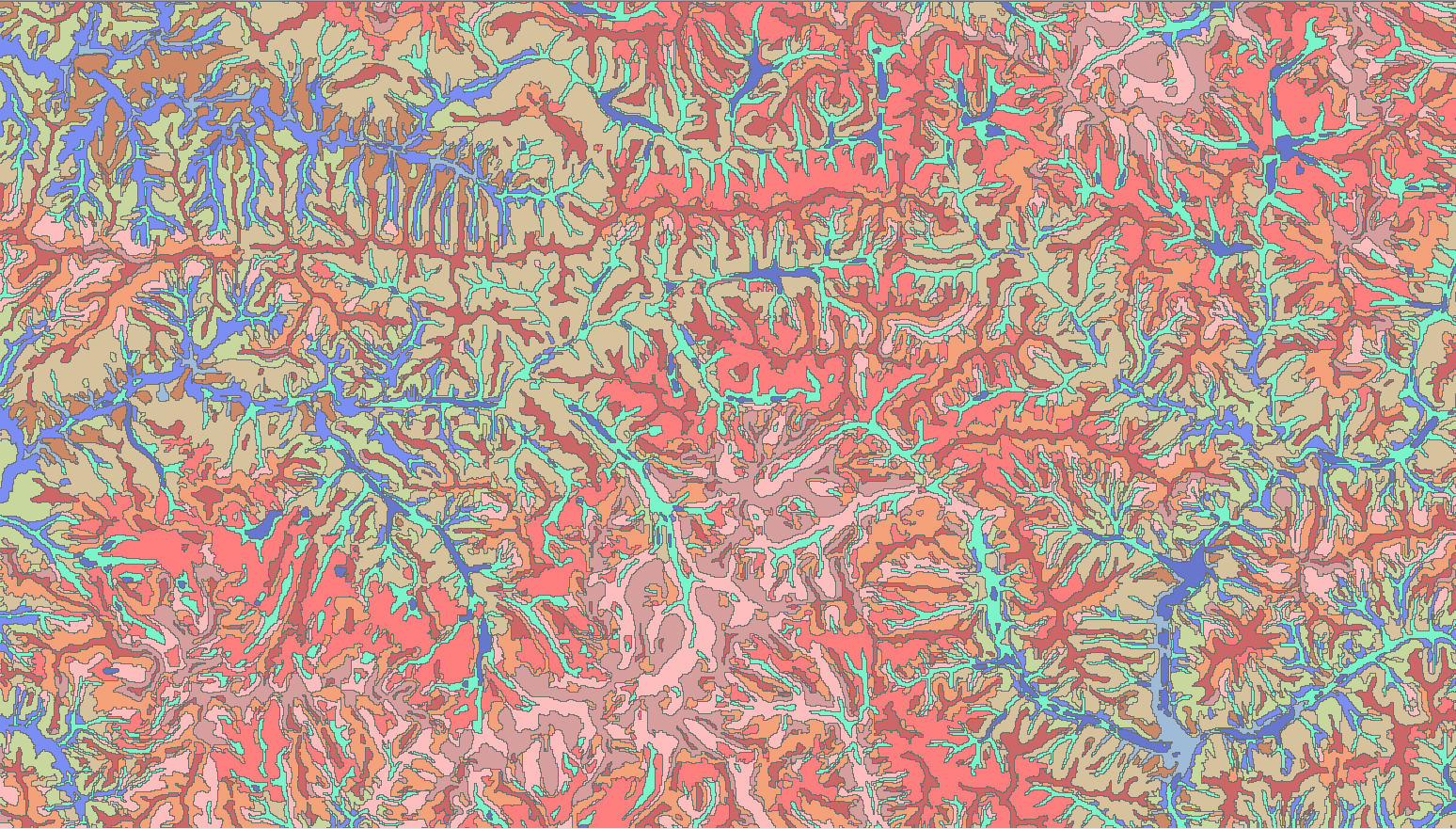
    Рис. 13.24 Relief Segmentation - кластеризации на 12 классов для территории природного парка Ергаки

    13.4. Методы "машинного" обучения и нейронные сети в классификации рельефа

    Развитие методов "машинного" обучения и алгоритмов нейросетей не могло не коснуться и всегда актуальной и востребованной на практике проблемы сегментации рельефа земной поверхности. Инструмент Geomorphones SAGA GIS (Terrain Analysis>>Lighting-Visibility) пример практически практически полностью автоматизированного алгоритма с получением так называемых геоморфонов - элементарных поверхностей или (в зависимости от масштаба) мезоформ рельефа [Stepinski, Jasiewicz, 2011].

    Инструмент - типичный "черный ящик" (machine vision approach), на входе только файл высот Elevation на выходе - растр Geomorphons - геоморфоны, регулируемые опции: Threshold Angle|Пороговое значение уклона для плоскости (по умолчанию 1o); Radial Limit|Дистанция расчета - дефолтное значение 1000, эту опцию можно менять в зависимости от размера и масштаба сцены методом "проб и ошибок"; Method - критически важный параметр выбора одного из двух методов расчета Line Tracing|Линейный или Multi Scale|Мультмасштабный, в последнем случае предполагается возможность учета "фрактального числа.

    В алгоритме инструмента Geomorphones заложена важная возможность изменения окрестностей расчета, связанных с размещением угловых точек неправильного многоугольника на характеристических точках рельефа, обладающих свойством положительной открытости. Конфигурация неправильных восьмиугольников определяются по принципу прямой видимости в восьми основных румбов компаса (поочередно между каждой парой угловых точек a и b - они определяют фактический масштаб, в пределах которого делимитируется элементы рельефа [Jasiewicz, Stepinski, 2013].


    Рис. 13.25 Геоморфоны: a) по алгоритму line tracing, b) по алгоритму multi scale

    Несмотря на то, что шкала легенды Geomorphons непрерывная, на самом деле перед нами атрибутированный растр с девятью значениями (где значения от 1 до 3 - привершинные поверхности, 9 - днища пойм и долин, 8 и 7 - боковые эрозионные формы, остальные значения 2,4,5,6 - склоны).

    Можно видеть, что различия в алгоритмах сказываются на большей выраженности склонов в способе line tracing, и в акцентировании привершинных и прикилевых поверхностей в способе multi scale.

    Таким образом, современные методы ГИС-моделирования предлагают достаточно широкий выбор алгоритмов различной сложности и разной степенью автоматизированности и участия эксперта. При этом на сегодняшний день лучший результат обеспечивают методы, основанные на кластерном анализе - Terrain Surface Classification, Terrain Clustering, K-means кластеризации с самостоятельным выбором факторов, Relief Segmentation.


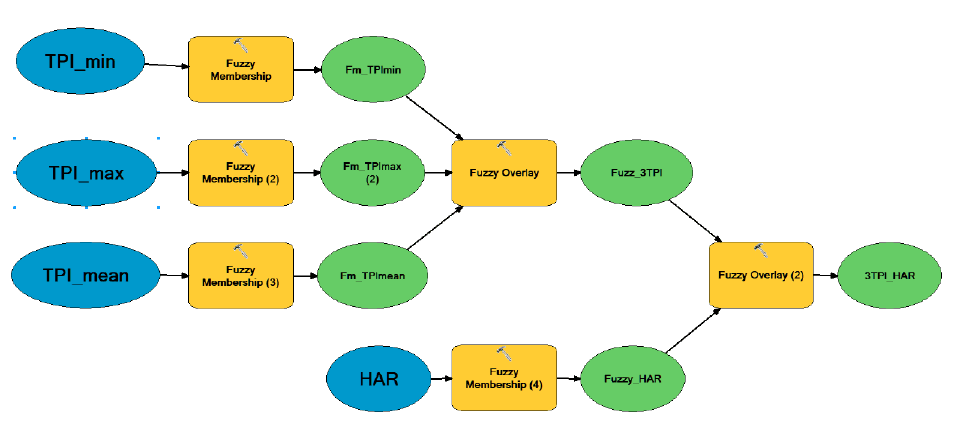
    Рис. 13.26 Усовершенствованный алгоритм Fuzzy Overlay с добавлением переменной TPI третьей размерности и растром относительной высоты

    Важно подчеркнуть, что современные средства моделирования, предоставленные пользователю в рамках практически всех популярных ГИС, позволяют экспериментировать с алгоритмами, добавляя или заменяя входные переменные, либо встраивая дополнительные процедуры. Так алгоритм Fuzzy overlay, основанный на сочетании разномасштабных индексов топографической позиции может быть оптимизирован добавлением третьего растра TPI (третьей переменной топографического индекса), а также переменной, так или иначе отображающей относительную высоту местоположения Height above river, Height above channels (Рис. 13.26).